函数
的部分图象如图所示
(1)求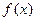 的最小正周期及解析式;
的最小正周期及解析式;
(2)设 求函数
求函数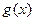 在区间
在区间 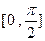 上的最大值和最小值.
上的最大值和最小值.
数列 的前n项和为
的前n项和为 ,存在常数A,B,C,使得
,存在常数A,B,C,使得 对任意正整数n都成立.
对任意正整数n都成立.
⑴若数列 为等差数列,求证:3A B+C=0;
为等差数列,求证:3A B+C=0;
⑵若 设
设 数列
数列 的前n项和为
的前n项和为 ,求
,求 ;
;
⑶若C=0, 是首项为1的等差数列,设
是首项为1的等差数列,设 数列
数列 的前2014项和为P,求不超过P的最大整数的值.
的前2014项和为P,求不超过P的最大整数的值.
要制作一个如图的框架(单位:m),要求所围成的总面积为19.5(m2),其中ABCD是一个矩形,EFCD是一个等腰梯形,梯形高h= AB,tan∠FED=
AB,tan∠FED= ,设AB=xm,BC=ym.
,设AB=xm,BC=ym.
(1)求y关于x的表达式;
(2)如何设计x、y的长度,才能使所用材料最少?
已知△ABC外接圆半径R=1,且 .
.
(1)求角 的大小; (2)求△ABC面积的最大值.
的大小; (2)求△ABC面积的最大值.
设等比数列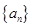 的前
的前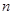 项和为
项和为 ,已知
,已知 成等差数列,(1)求数列
成等差数列,(1)求数列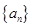 的公比
的公比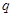 ,(2)若
,(2)若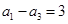 ,求
,求 ,并讨论
,并讨论 的最大值
的最大值
设锐角 的内角
的内角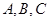 的对边分别为
的对边分别为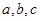 ,
,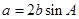 ,
,
(1)求角 大小(2)若
大小(2)若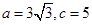 ,求
,求 边上的高
边上的高