如图,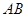 是底部
是底部 不可到达的一个塔型建筑物,
不可到达的一个塔型建筑物,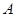 为塔的最高点.现需在对岸测出塔高
为塔的最高点.现需在对岸测出塔高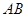 ,甲、乙两同学各提出了一种测量方法.
,甲、乙两同学各提出了一种测量方法.
甲同学的方法是:选与塔底 在同一水平面内的一条基线
在同一水平面内的一条基线 ,使
,使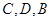 三点不在同一
三点不在同一
条直线上,测出 及
及 的大小(分别用
的大小(分别用 表示测得的数据)以及
表示测得的数据)以及 间的距离(用
间的距离(用 表示测得的数据),另外需在点
表示测得的数据),另外需在点 测得塔顶
测得塔顶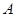 的仰角(用
的仰角(用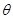 表示测量的数据),就可以求得塔高
表示测量的数据),就可以求得塔高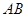 .
.
乙同学的方法是:选一条水平基线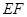 ,使
,使 三点在同一条直线上.在
三点在同一条直线上.在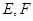 处分别测得塔顶
处分别测得塔顶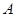 的仰角(分别用
的仰角(分别用 表示测得的数据)以及
表示测得的数据)以及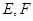 间的距离(用
间的距离(用 表示测得的数据),就可以求得塔高
表示测得的数据),就可以求得塔高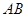 .
.
请从甲或乙的想法中选出一种测量方法,写出你的选择并按如下要求完成测量计算:①画出测量示意图;②用所叙述的相应字母表示测量数据,画图时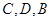 按逆时针方向标注,
按逆时针方向标注,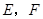 按从左到右的方向标注;③求塔高
按从左到右的方向标注;③求塔高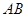 .
.
求一宇宙飞船的轨道,使在轨道上任一点处离地球和月球的视角都相等.
已知圆A的圆心在曲线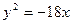 上,圆A与y轴相切,又与另一圆
上,圆A与y轴相切,又与另一圆 相外切,求圆A的方程.
相外切,求圆A的方程.
已知与曲线C: x2+y2-2x-2y+1=0相切的直线l与x轴、y轴的正半轴交于两点A、B,O为原点,|OA|=a,|OB|=b(a>2,b>2)
(1)求证:曲线C与直线l相切的条件是(a-2)(b-2)="2" ;
(2)求ΔAOB面积的最小值。
点A(0,2)是圆x2+y2=16内的定点,点B,C是这个圆上的两个动点,若BA⊥CA,求BC中点M的轨迹方程,并说明它的轨迹是什么曲线。
由点P(0,1)引圆x2+y2=4的割线l,交圆于A,B两点,使ΔAOB的面积为 (O为原点),求直线l的方程。
(O为原点),求直线l的方程。