（本小题满分15分）
在等比数列｛an｝中，首项为
，公比为
，
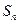表示其前n项和．
（I）记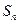=A，
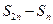= B，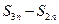
= C，证明A，B，C成等比数列；
（II）若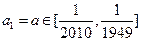
，
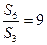，记数列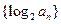
的前n项和为
，当n取何值时，有最小值．
数列
中，
，
，
．
（Ⅰ）证明：数列
是等比数列，并求
；
（Ⅱ）求数列
的前
项和
．
如图，在四棱锥
中，
平面
，
，
，
．
（Ⅰ）证明：
；
（Ⅱ）求
与平面
所成角的大小．
某项试验在甲、乙两地各自独立地试验两次，已知在甲、乙两地每次试验成功的概率依次为
、
；不成功的概率依次为
、
．
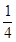（Ⅰ）求以上的四次试验中，至少有一次试验成功的概率；
（Ⅱ）在以上的四次试验中，试验成功的次数为
，求的分布列，并计算
．
在
中，角
、
、
所对的边依次为
、
、
，且
．
（Ⅰ）求
的值；
（Ⅱ）当的面积为
，且
时，求、、．
已知函数
=
，
=alnx，a
R。
（1） 若曲线y=与曲线y=相交，且在交点处有相同的切线，求a的值及该切线的方程；
（2）设函数h(x)= 
,当h(x)存在最小之时，求其最小值
的解析式；
（3）对（2）中的，证明：当a（0，+
）时，
1.