(本小题满分15分)
已知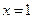 是函数
是函数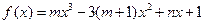 的一个极值点,其中
的一个极值点,其中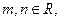
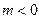 。
。
(Ⅰ)求 与
与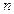 的关系表达式;
的关系表达式;
(Ⅱ)求 的单调区间;
的单调区间;
(Ⅲ)当 时,函数
时,函数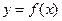 的图象上任意一点的切线斜率恒大于
的图象上任意一点的切线斜率恒大于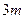 ,求实数
,求实数 的取值范围。
的取值范围。
设 是角
是角 终边上不同与原点O的一点,根据三角函数定义,求角
终边上不同与原点O的一点,根据三角函数定义,求角 的正弦、余弦、正切三角函数值.
的正弦、余弦、正切三角函数值.
已知椭圆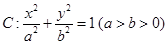 经过点(0,1),离心率
经过点(0,1),离心率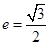 。
。
(1)求椭圆C的方程;
(2)设直线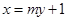 与椭圆C交于A、B两点,点A关于x轴的对称点为
与椭圆C交于A、B两点,点A关于x轴的对称点为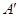 。
。
①试建立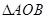 的面积关于m的函数关系;
的面积关于m的函数关系;
②某校高二(1)班数学兴趣小组通过试验操作初步推断;“当m变化时,直线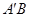 与x轴交于一个定点”。你认为此推断是否正确?若正确,请写出定点坐标,并证明你的结论;若不正确,请说明理由。
与x轴交于一个定点”。你认为此推断是否正确?若正确,请写出定点坐标,并证明你的结论;若不正确,请说明理由。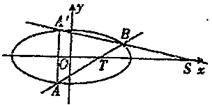
已知抛物线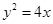 的焦点F,直线l过点
的焦点F,直线l过点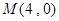 。
。
(1)若点F到直线l的距离为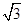 ,求直线l的斜率;
,求直线l的斜率;
(2)设A,B为抛物线上两点,且AB不与x轴垂直,若线段AB的垂直平分线恰过点M,求证:线段AB中点的横坐标为定值。
在平面直角坐标系xOy中,点P到两点 的距离之和等于4,设点P的轨迹为C。
的距离之和等于4,设点P的轨迹为C。
(1)求出C的轨迹方程;
(2)设直线 与C交于A、B两点,k为何值时
与C交于A、B两点,k为何值时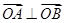 ?
?
已知 ,若
,若 是
是 必要而不充分条件,求实数m的取值范围。
必要而不充分条件,求实数m的取值范围。