(本小题满分12分)
设F是抛物线G: 的焦点,过F且与抛物线G的对称轴垂直的直线被抛物线G截得的线段长为4.
的焦点,过F且与抛物线G的对称轴垂直的直线被抛物线G截得的线段长为4.
(Ⅰ)求抛物线G的方程;
(Ⅱ)设A、B为抛物线G上异于原点的两点,且满足FA⊥FB,延长AF、BF分别交抛物线G于点C、D,求四边形ABCD面积的最小值.
在一次口试中,要从10道题中随机抽出3道题进行回答,答对了其中2道题就获得及格,某考生会回答10道题中的6道题,那么他(她)获得及格的概率是多少?
一个袋子里有4个不同的红球,6个不同的白球,从中任取4个使得取出的球中红球比白球多的取法有多少种?红球不少于白球的取法又有多少种?
(1)把5本不同的书分给3名同学,每人一本,有多少种不同的分法?
(2)把5本相同的书分给3名同学,每人一本,有多少种不同的分法?
(选修4-5;不等式选讲)若 与不等式
与不等式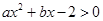 同解,
同解, 的解集为空集,求
的解集为空集,求 的取值范围.
的取值范围.
(选修4-4;坐标系与参数方程)已知直线 经过点P(1,1),倾斜角
经过点P(1,1),倾斜角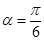 ,
,
(1)写出直线 的参数方程;
的参数方程;
(2)设 与圆
与圆 相交与两点A、B,求点P到A、B两点的距离之积.
相交与两点A、B,求点P到A、B两点的距离之积.