（本小题满分12分）某单位实行休年假制度三年以来，50名职工休年假的次数进行的调查统计结果如下表所示：
| 休假次数 |
 |
 |
 |
 |
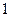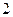| 人数 |
 |
 |
 |
 |
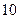根据上表信息解答以下问题：
（Ⅰ）从该单位任选两名职工，用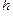
表示这两人休年假次数之和，记“函数
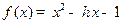在区间
，
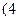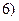上有且只有一个零点”为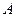事件
，求事件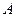发生的概率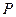
；
（Ⅱ）从该单位任选两名职工，用
表示这两人休年假次数之差的绝对值，求随机变量 的分布列及数学期望
．
（本小题满分12分）
对甲、乙两名自行车赛手在相同条件下进行了6次测试，测得他们的最大速度（m/s）的数据如下表.
（1）画出茎叶图，由茎叶图你能获得哪些信息？
（2）分别求出甲、乙两名自行车赛手最大速度（m/s）数据的平均数、中位数、标准差，并判断选谁参加比赛更合适.
（本小题满分10分）
甲、乙两人做出拳游戏（锤子、剪刀、布），求：
（1）平局的概率；
（2）甲赢的概率；
已知函数
在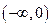
上是增函数，在
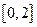上是减函数，且方程
有三个根，它们分别是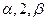
.
（1）求
的值；（2）求证： 
（3）求
的取值范围.
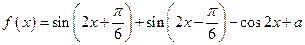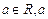已知函数
（
为常数）．
（1）求函数
的最小正周期和单调增区间；
（2）若函数的图像向左平移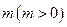
个单位后，得到函数
的图像关于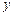
轴对称，求实数
的最小值
已知命题
：方程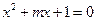
有两个不等的负根，命题
：
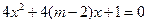无实根，若
或为真命题，且为假命题，求实数
的取值范围.