((本小题满分14分)
已知圆 ,点
,点 ,点
,点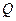 在圆
在圆 运动,
运动, 垂直平分线交
垂直平分线交 于点
于点 .
.
(Ⅰ)求动点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)设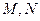 是曲线
是曲线 上的两个不同点,且点
上的两个不同点,且点 在第一象限,点
在第一象限,点 在第三象限,若
在第三象限,若 ,
,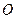 为坐标原点,求直线
为坐标原点,求直线 的斜率
的斜率 ;
;
(Ⅲ)过点 且斜率为
且斜率为 的动直线
的动直线 交曲线
交曲线 于
于 两点,在
两点,在 轴上是否存在定点
轴上是否存在定点 ,使以
,使以 为直径的圆恒过这个点?若存在,求出
为直径的圆恒过这个点?若存在,求出 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
某医院有内科医生12名,外科医生8名,现选派5名参加赈灾医疗队,其中
(1)某内科医生甲与某外科医生乙必须参加,共有多少种不同选法?
(2)甲、乙均不能参加,有多少种选法?
(3)甲、乙两人至少有一人参加,有多少种选法?
(4)队中至少有一名内科医生和一名外科医生,有几种选法?
某运输公司有7个车队.每个车队的车都多于4辆且型号相同,要从这7个车队中抽出10辆车组成一运输车队,每个车队至少抽1辆车,则不同抽法有多少种?
6个人进两间屋子,①每屋都进3人;②每屋至少进1人,问:各有多少种分配方法?
从5名女同学和4名男同学中选出4人参加演讲比赛,分别按下列要求,各有多少种不同的选法?
(1)男、女同学各2名;
(2)男、女同学分别至少有1名;
(3)在(2)的前提下,男同学甲与女同学乙不能同时选出.
求20Cn+55=4(n+4)Cn+3n-1+15An+32中n的值.