某大学毕业生参加一个公司的招聘考试,考试分笔试和面试两个环节,笔试有A、B两个题目,该学生答对A、B两题的概率分别为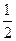 和
和 ,两题全部答对方可过入面试,面试要回答甲、乙两个题目,该学生答对这两个题目的概率均为
,两题全部答对方可过入面试,面试要回答甲、乙两个题目,该学生答对这两个题目的概率均为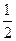 ,至少答对一题即可被聘用(假设每个环节的每个题目回答正确与否是相互独立的)
,至少答对一题即可被聘用(假设每个环节的每个题目回答正确与否是相互独立的)
(1)求该学生被公司聘用的概率;
(2)设该学生答对题目的个数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
设函数
.
(Ⅰ)证明:当
时,
;
(Ⅱ)设当
时,
,求
的取值范围.
己知斜率为1的直线
与双曲线
:
相交于
、
两点,且
的中点为
.
(Ⅰ)求
的离心率;
(Ⅱ)设
的右顶点为
,右焦点为
,
,证明:过
三点的圆与
轴相切.
如图,由
到
的电路中有4个元件,分别标为
,电流能通过
的概率都是
,电流能通过
的概率是0.9.电流能否通过各元件相互独立.已知
中至少有一个能通过电流的概率为0.999.
(Ⅰ)求
;
(Ⅱ)求电流能在
与
之间通过的概率;
(Ⅲ)
表示
中能通过电流的元件个数,求
的期望.
如图,直三棱柱
中,
,
,
为
的中点,
为
上的一点,
.
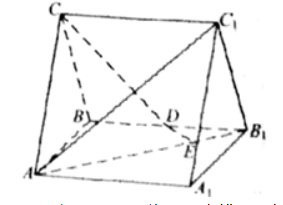
(Ⅰ)证明:
为异面直线
与
的公垂线;
(Ⅱ)设异面直线
与
的夹角为45°,求二面角
的大小.
已知数列
的前
项和
.
(Ⅰ)求
;
(Ⅱ)证明:
.