某班13位同学参加每周一次的卫生大扫除，按学校的卫生要求需要-优题课

某班13位同学参加每周一次的卫生大扫除，按学校的卫生要求需要完成总面积为80平方米的三个项目的任务，三个项目的面积比例和每人每分钟完成各项目的工作量如下图所示：
（1）从下面的统计图中可知：每人每分钟擦课桌椅 m2；擦玻璃、擦课桌椅、扫地拖地的面积分别是 m2， m2， m2；
（2）x人每分钟擦玻璃的面积是 m2（用x的式子表示）；
（3）他们一起完成扫地和拖地的任务后，把这13人分成两组，一组去擦玻璃，一组去擦课桌椅。如果你是卫生委员，这两组的人数该如何分配，才能最快地完成任务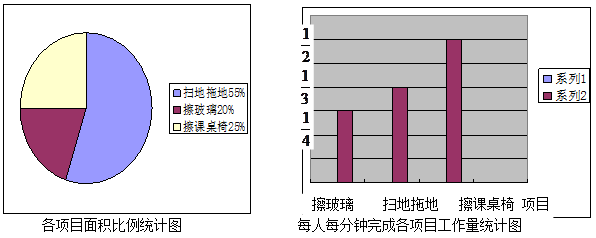

科目数学题型解答题难度较易

知识点：统计量的选择

目前，全球淡水资源分布不均、总量不足是人类面临的共同问题．某市在实施居民用水定额管理前，通过简单随机抽样对居民生活用水情况进行了调查，获得了若干个家庭去年的月均用水量数据（单位：t），整理出了频数分布表，频数分布直方图和扇形统计图，部分信息如下：

月均用水量（t）	$2 \leq x ＜ 3.5$	$3.5 \leq x ＜ 5$	$5 \leq x ＜ 6.5$	$6.5 \leq x ＜ 8$	$8 \leq x ＜ 9.5$
频数	$7$			$6$
对应的扇形区域	A	B	C	D	E

根据以上信息，解答下列问题：

（1）补全频数分布直方图，并求出扇形图中扇形E对应的圆心角的度数；

（2）为了鼓励节约用水，要确定一个用水量的标准，超出这个标准的部分按1.5倍价格收费，若要使该市60%的家庭水费支出不受影响，你觉得家庭月均用水量应该定为多少？并说明理由．

（1）计算： $2 \tan 60 ° + |\sqrt{3} - 2| +$ ${(\frac{1}{2022})}^{﹣ 1}$ $- \frac{\sqrt{12}}{2}$ ；

（2）先化简，再求值： $(\frac{x - y}{x} - \frac{x - 3 y}{x - y})$ $\div \frac{x + y}{x - y}$ ，其中 $x ＝ 1 ， y ＝ 100$ ．

在平面直角坐标系 $xOy$ 中，⊙ O 的半径为 1 ， A ， B 为⊙ O 外两点， $A B = 1$ ．给出如下定义：平移线段 AB ，得到⊙ O 的弦 $A^{'} B^{'}$ （ $A^{'}, B^{'}$ 分别为点 A ， B 的对应点），线段 $A A^{'}$ 长度的最小值称为线段 AB 到⊙ O 的"平移距离"．

（ 1 ）如图，平移线段 AB 到⊙ O 的长度为 1 的弦 $P_{1} P_{2}$ 和 $P_{3} P_{4}$ ，则这两条弦的位置关系是；在点 $P_{1}, P_{2}, P_{3}, P_{4}$ 中，连接点 A 与点的线段的长度等于线段 AB 到⊙ O 的"平移距离"；

（ 2 ）若点 A ， B 都在直线 $y = \sqrt{3} x + 2 \sqrt{3}$ 上，记线段 AB 到⊙ O 的"平移距离"为 $d_{1}$ ，求 $d_{1}$ 的最小值；

（ 3 ）若点 A 的坐标为 $(2, \frac{3}{2})$ ，记线段 AB 到⊙ O 的"平移距离"为 $d_{2}$ ，直接写出 $d_{2}$ 的取值范围．

在 $ΔABC$ 中， $∠ C = 90 °$ ， $AC > BC$ ， $D$ 是 $AB$ 的中点． $E$ 为直线 $AC$ 上一动点，连接 $DE$ ，过点 $D$ 作 $DF ⊥ DE$ ，交直线 $BC$ 于点 $F$ ，连接 $EF$ ．

（ 1 ）如图 1 ，当 $E$ 是线段 $AC$ 的中点时，设 $AE = a$ ， $BF = b$ ，求 $EF$ 的长（用含 $a, b$ 的式子表示）；

（ 2 ）当点 $E$ 在线段 $CA$ 的延长线上时，依题意补全图 2 ，用等式表示线段 $AE$ ， $EF$ ， $BF$ 之间的数量关系，并证明．

在平面直角坐标系 $xOy$ 中， $M (x_{1}, y_{1}), N (x_{2}, y_{2})$ 为抛物线 $y = a x^{2} + bx + c (a > 0)$ 上任意两点，其中 $x_{1} < x_{2}$ ．

（1）若抛物线的对称轴为 $x = 1$ ，当 $x_{1}, x_{2}$ 为何值时， $y_{1} = y_{2} = c;$

（2）设抛物线的对称轴为 $x = t$ ．若对于 $x_{1} + x_{2} > 3$ ，都有 $y_{1} < y_{2}$ ，求 $t$ 的取值范围．