甲、乙、丙三人进行象棋比赛,每两人比赛一场,共赛三场.每场比赛胜者得3
分,负者得0分,没有平局,在每一场比赛中,甲胜乙的概率为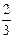 ,甲胜丙的概率为
,甲胜丙的概率为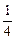 ,乙胜丙的概率为
,乙胜丙的概率为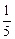
(1)求甲获第一名且丙获第二名的概率:
(2)设在该次比赛中,甲得分为ξ,求ξ的分布列和数学期望。
(本小题满分10分)选修4-4:坐标系与参数方程
已知极坐标的极点在平面直角坐标系的原点 处,极轴与
处,极轴与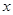 轴的正半轴重合,且长度单位相同.圆
轴的正半轴重合,且长度单位相同.圆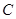 的参数方程为
的参数方程为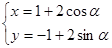 (
(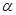 为参数),点
为参数),点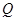 的极坐标为
的极坐标为 . (1)化圆
. (1)化圆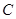 的参数方程为极坐标方程;
的参数方程为极坐标方程;
(2)若点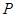 是圆
是圆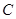 上的任意一点, 求
上的任意一点, 求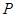 ,
,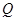 两点间距离的最小值.
两点间距离的最小值.
(本小题满分10分)选修4—1: 几何证明选讲
如图,直线 经过
经过 ⊙O上一点
⊙O上一点 ,且
,且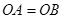 ,
, ,⊙O交直线
,⊙O交直线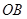 于
于 .
.
(1)求证:直线 是⊙O的切线;
是⊙O的切线;
(2)若 ⊙O的半径为3,求
⊙O的半径为3,求 的长.
的长.
已知函数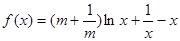 ,其中常数
,其中常数 .
.
(1)当 时,求函数
时,求函数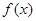 的极大值;
的极大值;
(2)试讨论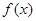 在区间
在区间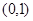 上的单调性;
上的单调性;
(3)当 时,曲线
时,曲线 上总存在相异两点
上总存在相异两点 ,
, ,使得曲线
,使得曲线 在点
在点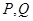 处的切线互相平行,求
处的切线互相平行,求 的取值范围.
的取值范围.
如图,在长方体 中
中 ,
,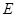 为
为 中点.
中点.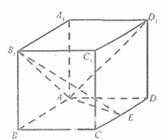
(1)求证: ;
;
(2)在棱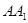 上是否存在一点
上是否存在一点 ,使得
,使得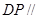 平面
平面 若存在,求
若存在,求 的长;若不存在,说明理由.
的长;若不存在,说明理由.
数列 满足
满足
(1)证明:数列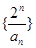 是等差数列; (2)求数列
是等差数列; (2)求数列 的通项公式
的通项公式 ;
;
(3)设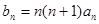 ,求数列
,求数列 的前
的前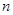 项和
项和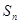 。
。