在菱形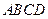 中,
中, ,线段
,线段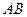 的中点是
的中点是 ,现将
,现将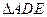 沿
沿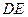 折起到
折起到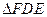 的位置,使平面
的位置,使平面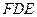 和平面
和平面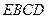 垂直,线段
垂直,线段 的中点是
的中点是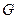 .
.
⑴证明:直线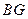 ∥平面
∥平面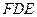 ;
;
⑵判断平面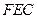 和平面
和平面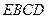 是否垂直,并证明你的结论.
是否垂直,并证明你的结论.
某工程要挖一个横断面为半圆的柱形的坑,挖出的土只能沿道路AP、BP运到P处(如图所示).已知PA="100" m,PB="150" m,∠APB=60°,试说明怎样运土最省工.
设有一颗彗星沿一椭圆轨道绕地球运行,地球恰好位于椭圆轨道的焦点处,当此彗星离地球相距m万千米和 m万千米时,经过地球和彗星的直线与椭圆的长轴夹角分别为
m万千米时,经过地球和彗星的直线与椭圆的长轴夹角分别为 和
和 ,求该彗星与地球的最近距离.
,求该彗星与地球的最近距离.
设F(1,0),点M在x轴上,点P在y轴上,且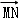 =2
=2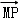 ,
,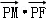 =0;
=0;
(1)当点P在y轴上运动时,求点N的轨迹C的方程;
(2)设A(x1,y1),B(x2,y2),D(x3,y3)是曲线C上除去原点外的不同三点,且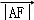 ,
,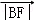 ,
,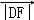 成等差数列,当线段AD的垂直平分线与x轴交于点E(3,0)时,求点B的坐标.
成等差数列,当线段AD的垂直平分线与x轴交于点E(3,0)时,求点B的坐标.
已知动圆M经过点A(3,0),且与直线l:x=﹣3相切,求动圆圆心M的轨迹方程.
根据下列条件写出抛物线的标准方程:
(1)准线方程是y=3;
(2)过点P(﹣2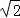 ,4);
,4);
(3)焦点到准线的距离为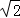 .
.