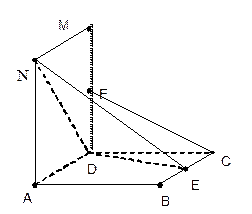.(本小题满分13分)
某创业投资公司拟投资开发某种新能源产品，估计能获得10万元～1000万元的投资收益.现准备制定一个对科研课题组的奖励方案：奖金y（单位：万元）随投资收益x（单位：万元）的增加而增加，且奖金不超过9万元，同时奖金不超过投资收益的20%.
（1）若建立函数f(x)模型制定奖励方案，试用数学语言表述公司对奖励函数f(x)模型
的基本要求；
（2）现有两个奖励函数模型：(1)y＝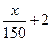
；(2)y＝4lgx－3.试分析这两个函数模型
是否符合公司要求？
求函数f(x)=
-2的极值。
已知椭圆C的焦点F1（－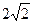
，0）和F2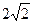（，0），长轴长6，设直线
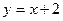交椭圆C于A
B两点，求线段AB的中点坐标
已知函数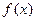
＝
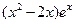（e为自然对数的底数）
（Ⅰ）求函数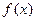单调递增区间；
（Ⅱ）若
,求函数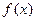在区间[0，
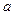]上的最大值和最小值．
(III)若函数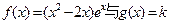
的图象有三个不同的交点，求实数k的取值范围.
(参考数据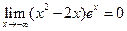
)
已知动点P与双曲线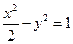
的两个焦点F1，F2的距离之和为定值，
且cos∠F1PF2的最小值为－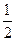
.
（1）求动点P的轨迹方程；
（2）是否存在直线l与P点轨迹交于不同的两点M、N，且线段MN恰被直线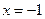
平分？若存在，求出直线l的斜率k的取值范围，若不存在说明理由.
如图，已知正方体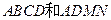
边长都为2，且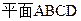
，
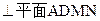E是BC的中点，F是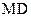
的中点，
（1）求证：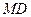
。
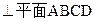(2)求点A到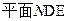
的距离。
(3)求证：CF∥。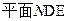
(4) 求二面角E－ND－A的平面角大小的
余弦值。