(本小题满分14分)
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
(1)证明 PA//平面EDB;
(2)证明PB⊥平面EFD;
(3)求二面角C-PB-D的大小.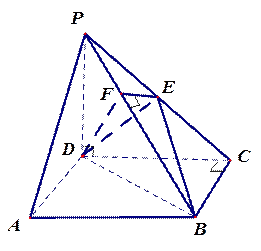
已知tan(α+ )=-3,α∈(0,
)=-3,α∈(0,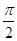 ).
).
(1)求tanα的值;
(2)求sin(2α- )的值.
)的值.
已知圆
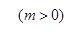 与抛物线
与抛物线 相交于
相交于 ,
, 两点
两点
(Ⅰ)求圆 的半径,抛物线的焦点坐标及准线方程;
的半径,抛物线的焦点坐标及准线方程;
(Ⅱ)设 是抛物线上不同于
是抛物线上不同于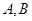 的点,且在圆外部,
的点,且在圆外部, 的延长线交圆于点
的延长线交圆于点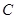 ,直线
,直线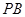 与
与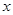 轴交于点
轴交于点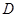 ,点
,点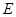 在直线
在直线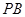 上,且四边形
上,且四边形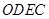 为等腰梯形,求点
为等腰梯形,求点 的坐标.
的坐标.
已知函数 .
.
(I)当a=3时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(II)对任意b>0,f(x)在区间[b-lnb,+∞)上是增函数,求实数a的取值范围.
在平面四边形ABCD中, ABC为正三角形,
ABC为正三角形, ADC为等腰直角三角形,AD=DC=2,将
ADC为等腰直角三角形,AD=DC=2,将 ABC沿AC折起,使点B至点P,且PD=2
ABC沿AC折起,使点B至点P,且PD=2 ,M为PA的中点,N在线段PD上。
,M为PA的中点,N在线段PD上。
(I)若PA 平面CMN,求证:AD//平面CMN;
平面CMN,求证:AD//平面CMN;
(II)求直线PD与平面ACD所成角的余弦值。
己知等比数列{ }的公比为q,前n项和为Sn,且S1,S3,S2成等差数列.
}的公比为q,前n项和为Sn,且S1,S3,S2成等差数列.
(I)求公比q;
(II)若 ,问数列{Tn}是否存在最大项?若存在,求出该项的值;若不存在,请说明理由。
,问数列{Tn}是否存在最大项?若存在,求出该项的值;若不存在,请说明理由。