((本小题满分12分)
如图所示,多面体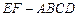 中,
中,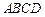 是梯形,
是梯形,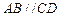 ,
, 是矩形,平面
是矩形,平面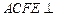 平面
平面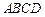 ,
, ,
,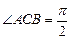 。
。
(1)求证: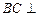 平面
平面 ;
;
(2)若 是棱
是棱 上一点,
上一点,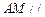 平面
平面 ,求
,求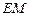 ;
;
(3)求二面角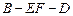 的平面角的余弦值。
的平面角的余弦值。
医生的专业能力参数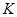 可有效衡量医生的综合能力,
可有效衡量医生的综合能力,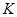 越大,综合能力越强,并规定: 能力参数
越大,综合能力越强,并规定: 能力参数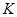 不少于30称为合格,不少于50称为优秀.某市卫生管理部门随机抽取300名医生进行专业能力参数考核,得到如图所示的能力
不少于30称为合格,不少于50称为优秀.某市卫生管理部门随机抽取300名医生进行专业能力参数考核,得到如图所示的能力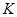 的频率分布直方图:
的频率分布直方图: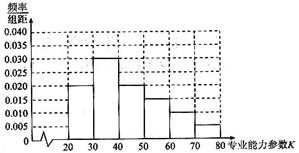
(Ⅰ)求出这个样本的合格率、优秀率;
(Ⅱ)现用分层抽样的方法从中抽出一个样本容量为20的样本,再从这20名医生中随机选出2名.
①求这2名医生的能力参数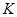 为同一组的概率;
为同一组的概率;
②设这2名医生中能力参数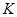 为优秀的人数为
为优秀的人数为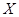 ,求随机变量
,求随机变量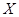 的分布列和期望.
的分布列和期望.
已知点M到点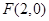 的距离比到点M到直线
的距离比到点M到直线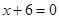 的距离小4;
的距离小4;
(Ⅰ)求点M的轨迹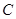 的方程;
的方程;
(Ⅱ)若曲线C上存在两点A,B关于直线l: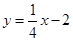 对称,求直线AB的方程
对称,求直线AB的方程
已知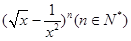 展开式中各项的二项式系数和比各项的系数和大256;
展开式中各项的二项式系数和比各项的系数和大256;
(Ⅰ)求展开式中的所有无理项的系数和;
(Ⅱ)求展开式中系数最大的项.
已知 恒成立,
恒成立,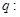 方程
方程 表示焦点在
表示焦点在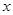 轴上的椭圆,若命题“
轴上的椭圆,若命题“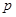 且
且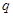 ”为假,求实数
”为假,求实数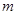 的取值范围.
的取值范围.
(本小题满分10分)选修4—5:不等式选讲
已知实数 满足
满足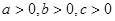 ,且
,且 .
.
(Ⅰ)证明: ;
;
(Ⅱ)证明: .
.