医生的专业能力参数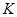 可有效衡量医生的综合能力,
可有效衡量医生的综合能力,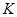 越大,综合能力越强,并规定: 能力参数
越大,综合能力越强,并规定: 能力参数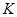 不少于30称为合格,不少于50称为优秀.某市卫生管理部门随机抽取300名医生进行专业能力参数考核,得到如图所示的能力
不少于30称为合格,不少于50称为优秀.某市卫生管理部门随机抽取300名医生进行专业能力参数考核,得到如图所示的能力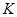 的频率分布直方图:
的频率分布直方图: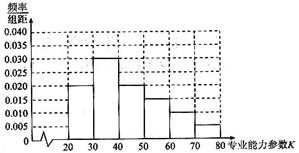
(Ⅰ)求出这个样本的合格率、优秀率;
(Ⅱ)现用分层抽样的方法从中抽出一个样本容量为20的样本,再从这20名医生中随机选出2名.
①求这2名医生的能力参数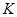 为同一组的概率;
为同一组的概率;
②设这2名医生中能力参数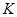 为优秀的人数为
为优秀的人数为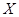 ,求随机变量
,求随机变量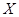 的分布列和期望.
的分布列和期望.
设
是单位圆
上的任意一点,
是过点
与
轴垂直的直线,
是直线
与
 轴的交点,点
在直线
上,且满足
. 当点
在圆上运动时,记点
的轨迹为曲线
.
(Ⅰ)求曲线
的方程,判断曲线
为何种圆锥曲线,并求其焦点坐标;
(Ⅱ)过原点且斜率为
的直线交曲线
于
,
两点,其中
在第一象限,它在
轴上的射影为点
,直线
交曲线
于另一点
. 是否存在
,使得对任意的
,都有
?若存在,求
的值;若不存在,请说明理由.
根据以往的经验,某工程施工期间的降水量
(单位:
)对工期的影响如下表:
| 降水量 | ||||
| 工期延误天数 | 0 |
2 |
6 |
10 |
历年气象资料表明,该工程施工期间降水量
小于300,700,900的概率分别为0.3,0.7,0.9. 求:
(Ⅰ)工期延误天数
的均值与方差;
(Ⅱ)在降水量X至少是300的条件下,工期延误不超过6天的概率.
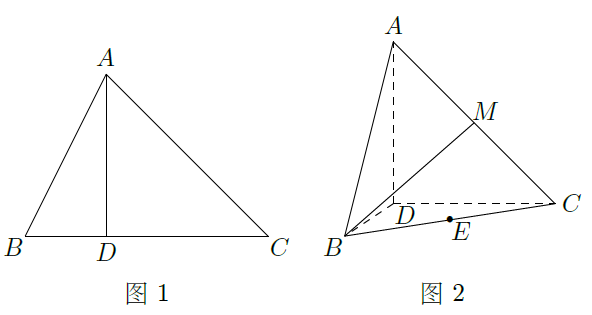
如图1,
,过动点
作
,垂足
在线段
上且异于点
,连接
,沿
将
折起,使
(如图2所示).
(Ⅰ)当
的长为多少时,三棱锥
的体积最大;
(Ⅱ)当三棱锥
的体积最大时,设点
分别为棱
的中点,试在棱
上确定一点
,使得
,并求
与平面
所成角的大小.
已知等差数列
前三项的和为
,前三项的积为
.
(Ⅰ)求等差数列
的通项公式;
(Ⅱ)若
,
,
成等比数列,求数列
的前
项和
已知向量
,
,设函数
的图象关于直线
对称,其中
,
为常数,且
.
(Ⅰ)求函数
的最小正周期;
(Ⅱ)若
的图象经过点
,求函数
在区间
上的取值范围.