已知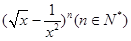 展开式中各项的二项式系数和比各项的系数和大256;
展开式中各项的二项式系数和比各项的系数和大256;
(Ⅰ)求展开式中的所有无理项的系数和;
(Ⅱ)求展开式中系数最大的项.
(本小题满分12分)有一种密码,明文是由三个字符组成,密码是由明文对应的五个数字组成,编码规则如下表:明文由表中每一排取一个字符组成,且第一排取的字符放在第一位,第二排取的字符放在第二位,第三排取的字符放在第三位,对应的密码由明文对应的数字按相同的次序排成一排组成.
第一排 |
明文字符 |
A |
B |
C |
D |
| 密码字符 |
11 |
12 |
13 |
14 |
|
第二排 |
明文字符 |
E |
F |
G |
H |
| 密码字符 |
21 |
22 |
23 |
24 |
|
第三排 |
明文字符 |
M |
N |
P |
Q |
| 密码字符 |
1 |
2 |
3 |
4 |
设随机变量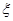 表示密码中不同数字的个数.
表示密码中不同数字的个数.
(Ⅰ)求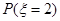 ; (Ⅱ)求随机变量
; (Ⅱ)求随机变量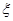 的分布列和它的数学期望.
的分布列和它的数学期望.
已知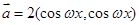 ,
, (其中
(其中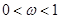 ),函数
),函数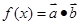 ,若直线
,若直线 是函数
是函数 图象的一条对称轴.
图象的一条对称轴.
(Ⅰ)试求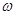 的值;
的值;
(Ⅱ)若函数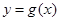 的图象是由
的图象是由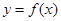 的图象的各点的横坐标伸长到原来的2倍,然后再向左平移
的图象的各点的横坐标伸长到原来的2倍,然后再向左平移 个单位长度得到,求
个单位长度得到,求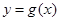 的单调递增区间.
的单调递增区间.
如图,已知椭圆C: 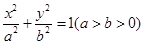 的左、右焦点分别为
的左、右焦点分别为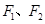 ,离心率为
,离心率为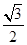 ,点A是椭圆上任一点,
,点A是椭圆上任一点,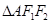 的周长为
的周长为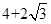 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点 任作一动直线l交椭圆C于
任作一动直线l交椭圆C于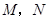 两点,记
两点,记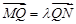 ,若在线段
,若在线段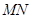 上取一点R,使得
上取一点R,使得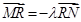 ,则当直线l转动时,点R在某一定直线上运动,求该定直线的方程.
,则当直线l转动时,点R在某一定直线上运动,求该定直线的方程.
设函数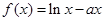 .
.
(Ⅰ)求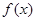 的单调区间;
的单调区间;
(Ⅱ)若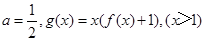 ,且
,且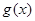 在区间
在区间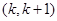 内存在极值,求整数
内存在极值,求整数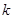 的值.
的值.
某高校组织的自主招生考试,共有1000名同学参加笔试,成绩均介于60分到100分之间,从中随机抽取50名同学的成绩进行统计,将统计结果按如下方式分为4组:第1组[60,70),第2组[70,80),第3组[80,90),第4组[90,100].如图是按上述分组方法得到的频率分布直方图,且笔试成绩在85分(含85分)以上的同学有面试资格.
(Ⅰ)估计所有参加笔试的1000名同学中,有面试资格的人数;
(Ⅱ)已知某中学有甲、乙两位同学取得面试资格,且甲的笔试比乙的高;面试时,要求每人回答两个问题,假设甲、乙两人对每一个问题答对的概率均为 ;若甲答对题的个数不少于乙,则甲比乙优先获得高考加分资格.求甲比乙优先获得高考加分资格的概率.
;若甲答对题的个数不少于乙,则甲比乙优先获得高考加分资格.求甲比乙优先获得高考加分资格的概率.