如图，已知椭圆C：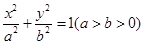 
的左、右焦点分别为
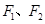，离心率为
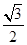，点A是椭圆上任一点，
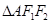的周长为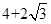
.
（Ⅰ）求椭圆C的方程；
（Ⅱ）过点
任作一动直线l交椭圆C于
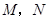两点，记
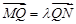，若在线段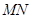
上取一点R，使得
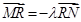，则当直线l转动时，点R在某一定直线上运动，求该定直线的方程.
(本题满分10分)选修4－1：几何证明选讲
如图,圆O的直径AB=10,弦DE⊥AB于点H,AH=2．
(1)求DE的长；
(2)延长ED到P，过P作圆O的切线，切点为C，若PC＝2
，求PD的长.
(本题满分12分)已知椭圆
的一个焦点是(1,0),两个焦点与短轴的一个端点构成等边三角形.
(1)求椭圆C的方程；
(2)过点(4,0)且不与坐标轴垂直的直线
交椭圆
于
、
两点,设点关于
轴的对称点为
.求证:直线
过轴上的一定点,并求出此定点坐标.
(本题满分12分)
已知函数
.
(1)求
的单调区间；
(2)若不等式
对任意
恒成立,求a的范围.
.(本题满分12分)
甲、乙两位学生参加数学竞赛培训.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下：
甲: 82 81 79 78 95 88 93 84
乙: 92 95 80 75 83 80 90 85
(1)画出甲、乙两位学生成绩的茎叶图,求出甲学生成绩的平均数以及乙学生成绩的中位数；
(2)若将频率视为概率,对甲学生在今后的三次数学竞赛成绩进行预测,记这三次成绩中高于80分的次数为
,求的分布列及数学期望
.
已知等差数列
的公差大于0,且
是方程
的两根，数列
的前
项的和为
,且
．
(1)求数列、的通项公式；
(2)设
,求数列
的前项和.