.(本题满分12分)
甲、乙两位学生参加数学竞赛培训.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲: 82 81 79 78 95 88 93 84
乙: 92 95 80 75 83 80 90 85
(1)画出甲、乙两位学生成绩的茎叶图,求出甲学生成绩的平均数以及乙学生成绩的中位数;
(2)若将频率视为概率,对甲学生在今后的三次数学竞赛成绩进行预测,记这三次成绩中高于80分的次数为 ,求
,求 的分布列及数学期望
的分布列及数学期望 .
.
( 12分 )如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形. 
(1)求证:DM∥平面APC;
(2)求证:平面ABC⊥平面APC;
(3)若BC=4,AB=20,求三棱锥D-BCM的体积.
( 12分 )已知汽车从刹车到停车所滑行的距离s(m)与速度v( m/s)的平方及汽车的总重量t(t)的乘积成正比.设某辆卡车不装货物以50 m/s行驶时,从刹车到停车滑行了20 m.如果这辆车装载着与车身相等重量的货物行驶,并与前面的车辆距离为15 m(假设卡车司机从发现前面车辆停车到自己刹车需耽搁1 s),为了保证前面车辆紧急停车时不与后面车辆撞车,最大限制速度是多少?
设关于 的函数
的函数 的最大值为
的最大值为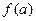
(1)求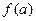 的表达式
的表达式
(2)确定使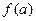 =5的
=5的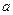 的值,并对此时的
的值,并对此时的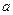 ,求
,求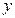 的最小值
的最小值
已知函数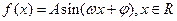 (其中
(其中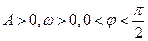 )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为 ,且图象上一个最低点为
,且图象上一个最低点为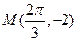 .
.
(1)求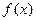 的解析式;
的解析式;
(2)用五点作图法做出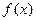 的图像
的图像
(3)说明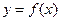 的图象是由
的图象是由 的图象经过怎样的变换得到
的图象经过怎样的变换得到
(4)求函数的单调递减区间
(5)当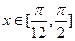 ,求
,求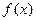 的值域.
的值域.
以一年为一个周期调查某商品出厂价格及该商品在商店的销售价格时发现:该商品的出厂价格是在6元基础上按月份随正弦曲线波动的,已知3月份出厂价格最高为8元,7月份出厂价格最低为4元,而该商品在商店的销售价格是在8元基础上按月随正弦曲线波动的,并已知5月份销售价最高为10元,9月份销售价最低为6元,假设某商店每月购进这种商品m件,且当月售完,请分别写出该商品的出厂价格函数、销售价格函数、盈利函数的解析式