( 12分 )已知汽车从刹车到停车所滑行的距离s(m)与速度v( m/s)的平方及汽车的总重量t(t)的乘积成正比.设某辆卡车不装货物以50 m/s行驶时,从刹车到停车滑行了20 m.如果这辆车装载着与车身相等重量的货物行驶,并与前面的车辆距离为15 m(假设卡车司机从发现前面车辆停车到自己刹车需耽搁1 s),为了保证前面车辆紧急停车时不与后面车辆撞车,最大限制速度是多少?
(本小题满分13分)已知点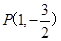 在椭圆
在椭圆 上,椭圆
上,椭圆 的左焦点为(-1,0)
的左焦点为(-1,0)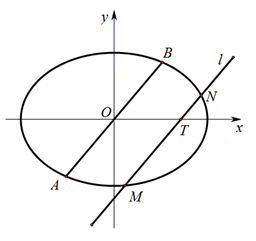
(1)求椭圆 的方程;
的方程;
(2)直线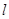 过点
过点 交椭圆C于M、N两点,AB是椭圆
交椭圆C于M、N两点,AB是椭圆 经过原点
经过原点 的弦,且MN//AB,问是否存在正数
的弦,且MN//AB,问是否存在正数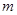 ,使
,使 为定值?若存在,求出
为定值?若存在,求出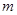 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(本小题满分12分)已知数列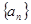 的前
的前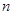 项和为
项和为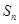 ,且
,且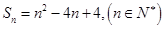
(1)求数列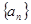 的通项公式;
的通项公式;
(2)数列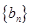 中,令
中,令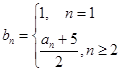 ,
, 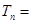
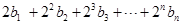 ,求
,求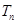 .
.
(本小题满分12分)如图,在底面是正方形的四棱锥P—ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.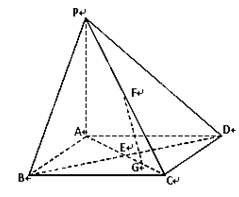
(1)求证:BD⊥FG;
(2)当二面角B—PC—D的大小为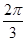 时,求PC与底面ABCD所成角的正切值.
时,求PC与底面ABCD所成角的正切值.
(本小题满分12分)在平面直角坐标系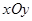 中,点
中,点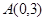 ,直线
,直线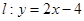 ,设圆
,设圆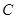 的半径为
的半径为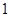 ,圆心在
,圆心在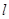 上.
上.
(1)若圆心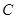 也在直线
也在直线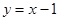 上,过点
上,过点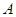 作圆
作圆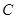 的切线,求切线的方程;
的切线,求切线的方程;
(2)若圆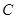 上存在点
上存在点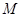 ,使
,使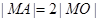 ,求圆心
,求圆心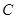 的横坐标
的横坐标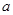 的取值范围.
的取值范围.
(本小题满分12分)在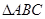 中,角
中,角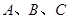 所对的边为
所对的边为 ,且满足
,且满足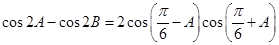
(1)求角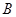 的值;
的值;
(2)若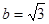 且
且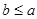 ,求
,求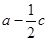 的取值范围.
的取值范围.