设双曲线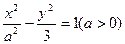 的两个焦点分别为
的两个焦点分别为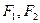 ,离心率为
,离心率为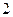 .
.
(I)求此双曲线的渐近线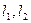 的方程;
的方程;
(II)若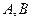 分别为
分别为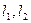 上的点,且
上的点,且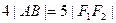 ,求线段
,求线段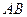 的中点
的中点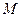 的轨迹方程,并说明轨迹是什么曲线.
的轨迹方程,并说明轨迹是什么曲线.
已知函数 的定义域为
的定义域为 ,若
,若 在
在 上为增函数,则称
上为增函数,则称 为“一阶比增函数”.
为“一阶比增函数”.
(Ⅰ) 若 是“一阶比增函数”,求实数
是“一阶比增函数”,求实数 的取值范围;
的取值范围;
(Ⅱ) 若 是“一阶比增函数”,求证:
是“一阶比增函数”,求证: ,
, ;
;
(Ⅲ)若 是“一阶比增函数”,且
是“一阶比增函数”,且 有零点,求证:
有零点,求证: 有解.
有解.
已知函数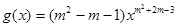 是幂函数且在
是幂函数且在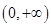 上为减函数,函数
上为减函数,函数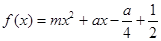 在区间
在区间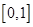 上的最大值为2,试求实数
上的最大值为2,试求实数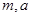 的值。
的值。
设函数 .
.
(I)当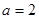 时,求
时,求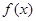 的单调区间;
的单调区间;
(II)若 对
对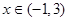 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知命题:“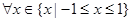 ,都有不等式
,都有不等式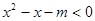 成立”是真命题。
成立”是真命题。
(I)求实数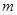 的取值集合
的取值集合 ;
;
(II)设不等式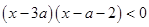 的解集为
的解集为 ,若
,若 是
是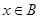 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围.
的取值范围.
函数f(x)=x2+x- .
.
(I)若定义域为[0,3],求f(x)的值域;
(II)若f(x)的值域为[-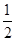 ,
, ],且定义域为[a,b],求b-a的最大值.
],且定义域为[a,b],求b-a的最大值.