(本小题满分12 分)
已知函数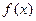 是定义在R上的不恒为零的函数,且对于任意的
是定义在R上的不恒为零的函数,且对于任意的 、
、 ∈R,都满足
∈R,都满足 ,若
,若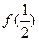 =1,
=1,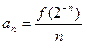 ;
;
(1)求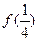 、
、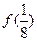 、
、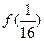 的值;
的值;
(2)猜测数列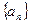 的通项公式,并用数学归纳法证明。
的通项公式,并用数学归纳法证明。
如图所示,直三棱柱ABC—A1B1C1中,B1C1=A1C1,AC1⊥A1B,M、N分别是A1B1、AB的中点.
(1)求证:C1M⊥平面A1ABB1;
(2)求证:A1B⊥AM;
(3)求证:平面AMC1∥平面NB1C;
(4)求A1B与B1C所成的角.
如图所示,在四棱锥P—ABCD中,底面为直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M、N分别为PC、PB的中点.
(1)求证:PB⊥DM;
(2)求BD与平面ADMN所成的角.
如图所示,已知PA⊥矩形ABCD所在平面,
M,N分别是AB,PC的中点.
(1)求证:MN⊥CD;
(2)若∠PDA=45°.求证:MN⊥平面PCD.
如图所示,在四棱锥P—ABCD中,底面ABCD是∠DAB=60°且边长为a的菱形,侧面PAD为正三角形,其所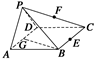 在平面垂直于底面ABCD,若G为AD边的中点,
在平面垂直于底面ABCD,若G为AD边的中点,
(1)求证:BG⊥平面PAD;
(2)求证:AD⊥PB;
(3)若E为BC边的中点,能否在棱PC上找到一点F,使平面DEF⊥平面ABCD,并证明你的结论.
如图所示,正四棱锥P—ABCD的各棱长均为13,M,N分别为PA,BD上的点,且PM∶MA=BN∶ND=5∶8.
(1)求证:直线MN∥平面PBC;
(2)求线段MN的长.