如图所示,在四棱锥P—ABCD中,底面为直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M、N分别为PC、PB的中点.
(1)求证:PB⊥DM;
(2)求BD与平面ADMN所成的角.
(本题12分)已知向量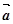 =(2cos θ,2sin θ),向量
=(2cos θ,2sin θ),向量 =(
=(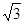 ,-1),则|2
,-1),则|2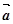 +
+ |的最大值.
|的最大值.
(本题10分)已知 ,试求
,试求 的值.
的值.
(本小题满分14分)已知椭圆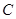 :
: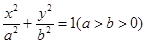 的焦距为4,其长轴长和短轴长之比为
的焦距为4,其长轴长和短轴长之比为 .
.
(Ⅰ)求椭圆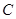 的标准方程;
的标准方程;
(Ⅱ)设 为椭圆
为椭圆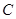 的右焦点,
的右焦点,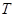 为直线
为直线 上纵坐标不为
上纵坐标不为 的任意一点,过
的任意一点,过 作
作 的垂线交椭圆
的垂线交椭圆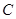 于点
于点 ,若
,若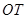 平分线段
平分线段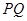 (其中
(其中 为坐标原点),求
为坐标原点),求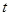 的值
的值
(本小题满分12分)如图,四棱锥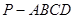 ,侧面
,侧面 是边长为2的正三角形,且与底面垂直,底面
是边长为2的正三角形,且与底面垂直,底面 是
是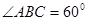 的菱形,
的菱形,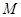 为
为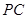 的中点.
的中点.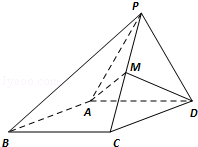
(Ⅰ)求证: 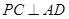 ;
;
(Ⅱ)在棱 上是否存在一点
上是否存在一点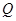 ,使得
,使得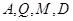 四点共面?若存在,指出点
四点共面?若存在,指出点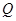 的位置并证明;若不存在,请说明理由;
的位置并证明;若不存在,请说明理由;
(Ⅲ)求点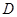 到平面
到平面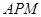 的距离.
的距离.
(本小题满分12分)已知定义在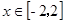 上的偶函数
上的偶函数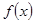 满足:当
满足:当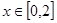 时,
时,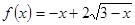 .
.
(1)求函数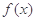 在
在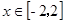 上的解析式;
上的解析式;
(2)设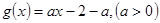 ,若对于任意
,若对于任意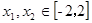 ,都有
,都有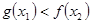 成立,求实数
成立,求实数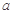 的取值范围.
的取值范围.