(1)如图①,若∠B+∠D=∠BED,试猜想AB与CD的位置关系,并说明理由。 
(2)如图②,要想得到AB∥CD,则∠1、∠2、∠3之间应满足怎样的位置关系?请探索。
二次函数图象的顶点在原点O,经过点A(1,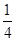 );点F(0,1)在y轴上.直线y=-1与y轴交于点H.
);点F(0,1)在y轴上.直线y=-1与y轴交于点H.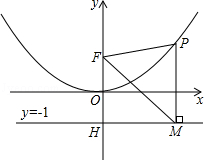
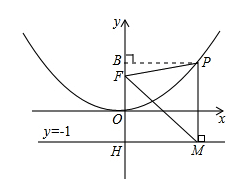
(1)求二次函数的解析式;
(2)点P是(1)中图象上的点,过点P作x轴的垂线与直线y=-1交于点M,求证:FM平分∠OFP;
(3)当△FPM是等边三角形时,求P点的坐标.
如图,在矩形ABCD中,AB=6,BC=8,动点P以2个单位/秒的速度从A点出发,沿对角线AC向C移动,同时动点Q以1个单位/秒的速度从C点出发,沿CB向点B移动,当其中有一点到达终点时,它们都停止移动.设移动的时间为t秒.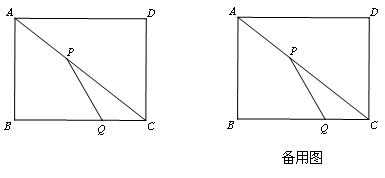
(1)求△CPQ的面积S与时间t之间的函数关系式;
(2)以P为圆心,PA为半径的圆与以Q为圆心,QC为半径的圆相切时,求出t的值.
(3)在P、Q移动的过程中,当△CPQ为等腰三角形时,直接写出t的值;
某果品批发公司以16元/千克购进一批樱桃.由往年市场销售情况的统计分析可知:当销售价定为25 元/千克时,每天可售出1 000 千克;若销售价定为20元/千克时,每天可售出2000千克.假设每天的销售量y(千克)与销售价x(元/千克)之间满足一次函数.
(1)试求y与x之间的函数关系式;
(2)在商品无积压且不考虑其他因素的条件下,销售价格定为多少时,才能使每天的销售毛利润W(元)最大?最大利润是多少?
七年级我们学过三角形的相关知识,在动手实践的过程中,发现了一个基本事实:
三角形的三条高(或三条高所在直线)相交于一点.
其实,有很多八年级、九年级的问题均可用此结论解决.
【运用】如图,已知:△ABC的高AD与高BE相交于点F,且∠ABC=45°,过点F作FG∥BC交AB于点G,求证:FG+CD=BD.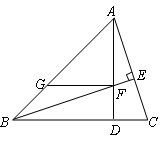
小方同学在解答此题时,利用了上述结论,她的方法如下:
连接CF并延长,交AB于点M,
∵△ABC的高AD与高BE相交于点F,
∴CM为△ABC的高.
(请你在下面的空白处完成小方的证明过程.)
【操作】如图AB是圆的直径,点C在圆内,请仅用无刻度的直尺画出△ABC中AB边上的高.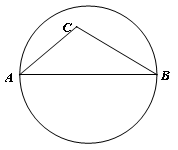
某花圃用花盆培育某种花苗,原来每盆植入3株花苗时,平均每株可盈利3元.经过试验发现若每盆多植入1株花苗,则平均每株盈利就减少0.5元.为使每盆培育花苗的盈利达到10元,则每盆应该植入花苗多少株?