如图所示,两根正对的平行金属直轨道MN、M´N´位于同一水平面上,两轨道之间的距离 l = 0.50m.轨道的MM′端之间接一阻值R =0.40Ω的定值电阻,NN′端与两条位于竖直面内的半圆形光滑金属轨道NP、N′P′平滑连接,两半圆轨道的半径均为 R0 = 0.50m.直轨道的右端处于竖直向 下、磁感应强度B = 0.64T的匀强磁场中,磁场区域的宽度d = 0.80m,且其右边界与NN′重合.现有一质量 m = 0.20kg、电阻 r = 0.10Ω的导体杆ab静止在距磁场的左边界s = 2.0m处.在与杆垂直的水平恒力 F =2.0N的作用下ab杆开始运动,当运动至磁场的左边界时撤去F,结果导体ab恰好能以最小速度通过半圆形轨道的最高点PP′.已知导体杆ab在运动过程中与轨道接触良好,且始终与轨道垂直,导体杆ab与直轨道之间的动摩擦因数 μ= 0.10,轨道的电阻可忽略不计,取 g = 10m/s2,求:
下、磁感应强度B = 0.64T的匀强磁场中,磁场区域的宽度d = 0.80m,且其右边界与NN′重合.现有一质量 m = 0.20kg、电阻 r = 0.10Ω的导体杆ab静止在距磁场的左边界s = 2.0m处.在与杆垂直的水平恒力 F =2.0N的作用下ab杆开始运动,当运动至磁场的左边界时撤去F,结果导体ab恰好能以最小速度通过半圆形轨道的最高点PP′.已知导体杆ab在运动过程中与轨道接触良好,且始终与轨道垂直,导体杆ab与直轨道之间的动摩擦因数 μ= 0.10,轨道的电阻可忽略不计,取 g = 10m/s2,求:
(1)导体杆刚进入磁场时,通过导体杆上的电流大小和方向;
(2)导体杆穿过磁场的过程中整个电路产生的焦耳热.

如图所示,MN、PQ是平行金属板,板长为L两板间距离为d,在PQ板的上方有垂直纸面向里足够大的匀强磁场.一个电荷量为q,质量为m的带负电粒子以速度V0从MN板边缘且紧贴M点,沿平行于板的方向射入两板间,结果粒子恰好从PQ板左边缘飞进磁场,然后又恰好从PQ板的右边缘飞进电场.不计粒子重力,求:
(1)两金属板间所加电压U的大小;
(2)匀强磁场的磁感应强度B的大小;
(3)当该粒子再次进入电场并再次从电场中飞出时的速度及方向.
如图,POy区域内有沿y轴正方向的匀强电场,POx区域内有垂直纸面向里的匀强磁场,OP与x轴成θ角.不计重力的负电荷,质量为m、电量为q,从y轴上某点以初速度v0垂直电场方向进入,经电场偏转后垂直OP进入磁场,又垂直x轴离开磁场.求:
(1)电荷进入磁场时的速度大小
(2)电场力对电荷做的功
(3)电场强度E与磁感应强度B的比值.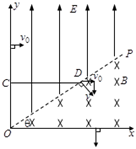
高频焊接是一种常用的焊接方法,图1是焊接的原理示意图。将半径r=0.10m的待焊接环形金属工件放在线圈中,然后在线圈中通以高频变化的电流,线圈产生垂直于工件平面的匀强磁场,磁场方向垂直线圈平面向里,磁感应强度B随时间t的变化规律如图2所示。工件非焊接部分单位长度上的电阻R0=1.0×10-3m-1,焊缝处的接触电阻为工件非焊接部分电阻的9倍。焊接的缝宽非常小,不计温度变化对电阻的影响。求: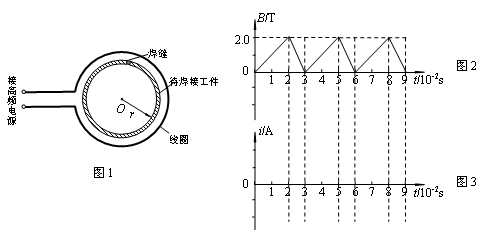
(1)0~2.010-2s和2.010-2s~3.010-2s时间内环形金属工件中感应电动势各是多大;
(2)0~2.010-2s和2.010-2s~3.010-2s时间内环形金属工件中感应电流的大小,并在图3中定量画出感应电流随时间变化的i-t图象(以逆时针方向电流为正);
(3)在t=0.10s内电流通过焊接处所产生的焦耳热。
(1)开普勒从1609年~1619年发表了著名的开普勒行星运动三定律,其中第一定律为:所有的行星分别在大小不同的椭圆轨道上围绕太阳运动,太阳在这个椭圆的一个焦点上。第三定律:所有行星的椭圆轨道的半长轴的三次方跟公转周期的平方的比值都相等.实践证明,开普勒三定律也适用于其他中心天体的卫星运动。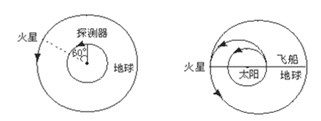
(2)从地球表面向火星发射火星探测器.设地球和火星都在同一平面上绕太阳做圆周运动,火星轨道半径Rm为地球轨道半径R0的1.5倍,简单而又比较节省能量的发射过程可分为两步进行:第一步,在地球表面用火箭对探测器进行加速,使之获得足够动能,从而脱离地球引力作用成为一个沿地球轨道运动的人造行星。第二步是在适当时刻点燃与探测器连在一起的火箭发动机,在短时间内对探测器沿原方向加速,使其速度数值增加到适当值,从而使得探测器沿着一个与地球轨道及火星轨道分别在长轴两端相切的半个椭圆轨道正好射到火星上.当探测器脱离地球并沿地球公转轨道稳定运行后,在某年3月1日零时测得探测器与火星之间的角距离为60°,如图所示,问应在何年何月何日点燃探测器上的火箭发动机方能使探测器恰好落在火星表面?(时间计算仅需精确到日),已知地球半径为: ;
; ;
;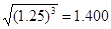
登山运动员在登雪山时要注意防止紫外线的过度照射��尤其是眼睛更不能长时间被紫外线照射,否则将会严重地损坏视力。有人想利用薄膜干涉的原理设计一种能大大减小紫外线对眼睛的伤害的眼镜。他选用的薄膜材料的折射率为n=1.5,所要消除的紫外线的频率为 Hz,那么它设计的这种“增反膜”的厚度至少是多少?
Hz,那么它设计的这种“增反膜”的厚度至少是多少?