甲、乙两篮球运动员 互不影响地在同一位置投球,命中率分别为
互不影响地在同一位置投球,命中率分别为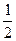 与
与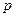 ,且乙投球2次均未命中的概率是
,且乙投球2次均未命中的概率是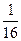 . 求:
. 求:
(1)乙投球的命中率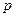 ;
;
(2)甲投球2次,至少命中1次的概率;
(3)若甲、乙二人各投球2次,求两人共命中2次的概率
已知递增等差数列 中的
中的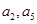 是函数
是函数 的两个零点.数列
的两个零点.数列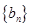 满足,点
满足,点 在直线
在直线 上,其中
上,其中 是数列
是数列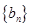 的前
的前 项和.
项和.
(Ⅰ)求数列 和
和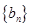 的通项公式;
的通项公式;
(Ⅱ)令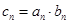 ,求数列
,求数列 的前n项和
的前n项和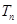 .
.
【原创】已知函数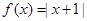 ,
,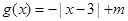 .
.
(Ⅰ)解关于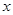 的不等式
的不等式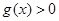 ;
;
(Ⅱ)若函数 的图象恒在函数
的图象恒在函数 图象的上方,求
图象的上方,求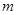 的取值范围.
的取值范围.
已知曲线C的极坐标方程为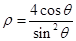 ,以极点为坐标原点,极轴为x轴正半轴建立平面直角坐标系,直线
,以极点为坐标原点,极轴为x轴正半轴建立平面直角坐标系,直线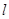 的参数方程为
的参数方程为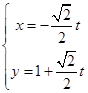 (t为参数).
(t为参数).
(Ⅰ)把曲线C的极坐标方程化为直角坐标方程,把直线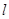 的参数方程化为普通方程;
的参数方程化为普通方程;
(Ⅱ)求直线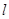 被曲线C截得的线段AB的长.
被曲线C截得的线段AB的长.
如图,四边形ABDC内接于圆,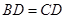 ,过C点的圆的切线与AB的延长线交于E点.
,过C点的圆的切线与AB的延长线交于E点.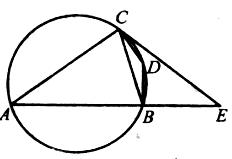
(Ⅰ)求证: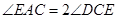 ;
;
(Ⅱ)若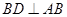 ,
,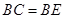 ,
,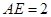 ,求AB的长.
,求AB的长.
已知函数 .
.
(Ⅰ)若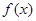 在区间
在区间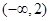 上为单调递增函数,求实数
上为单调递增函数,求实数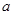 的取值范围;
的取值范围;
(Ⅱ)若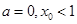 ,设直线
,设直线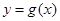 为函数
为函数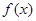 的图象在
的图象在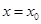 处的切线,求证:
处的切线,求证: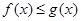 .
.