选修4—4:坐标系与参数方程
平面直角坐标系中,直线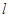 的参数方程是
的参数方程是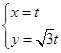 (
(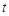 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,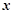 轴的正半轴为极轴,建立极坐标系,已知曲线
轴的正半轴为极轴,建立极坐标系,已知曲线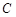 的极坐标方程为
的极坐标方程为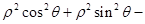
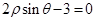 .
.
(Ⅰ)求直线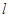 的极坐标方程;
的极坐标方程;
(Ⅱ)若直线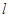 与曲线
与曲线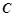 相交于
相交于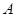 、
、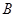 两点,求
两点,求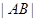 .
.
求关于x的方程x2-mx+3m-2=0的两根均大于1的充要条件.
证明一元二次方程ax2+bx+c=0有一正根和一负根的充要条件是ac<0.
写出下列命题的否命题,并判断原命题及否命题的真假:
(1)如果一个三角形的三条边都相等,那么这个三角形的三个角都相等;
(2)矩形的对角线互相平分且相等;
(3)相似三角形一定是全等三角形.
已知ab≠0,求证:a+b=1的充要条件是a3+b3+ab-a2-b2=0.
指出下列命题中,p是q的什么条件(在“充分不必要条件”、“必要不充分条件”、“充要条件”、“既不充分也不必要条件”中选出一种作答).
(1)在△ABC中,p:∠A=∠B,q:sinA=sinB;
(2)对于实数x、y,p:x+y≠8,q:x≠2或y≠6;
(3)非空集合A、B中,p:x∈A∪B,q:x∈B;
(4)已知x、y∈R,p:(x-1)2+(y-2)2=0,q:(x-1)(y-2)=0.