((本小题满分12分)
已知x>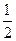 ,函数f(x)=
,函数f(x)= ,h(x)=2e lnx(e为自然常数).
,h(x)=2e lnx(e为自然常数).
(Ⅰ)求证:f(x)≥h(x);
(Ⅱ)若f(x)≥h(x)且g(x)≤h(x)恒成立,则称函数h(x)的图象为函数f(x),g(x)的“边界”.已知函数g(x)=-4 +px+q(p,q∈R),试判断“函数f(x),g(x)以函数h(x)的图象为边界”和“函数f(x),g(x)的图象有且仅有一个公共点”这两个条件能否同时成立?若能同时成立,请求出实数p、q的值;若不能同时成立,请说明理由.
+px+q(p,q∈R),试判断“函数f(x),g(x)以函数h(x)的图象为边界”和“函数f(x),g(x)的图象有且仅有一个公共点”这两个条件能否同时成立?若能同时成立,请求出实数p、q的值;若不能同时成立,请说明理由.
设 是曲线
是曲线 上的任一点,
上的任一点, 是曲线
是曲线 上的任一点,称
上的任一点,称 的最小值为曲线
的最小值为曲线 与曲线
与曲线 的距离.
的距离.
(1)求曲线 与直线
与直线 的距离;
的距离;
(2)设曲线 与直线
与直线 (
( )的距离为
)的距离为 ,直线
,直线 与直线
与直线 的距离为
的距离为 ,求
,求 的最小值.
的最小值.
如图,边长为2的正方形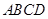 中,点
中,点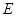 是
是 的中点,点
的中点,点 是
是 的中点,将△
的中点,将△ 、△
、△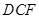 分别沿
分别沿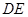 、
、 折起,使
折起,使 、
、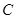 两点重合于点
两点重合于点 ,连接
,连接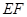 ,
,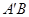 .
.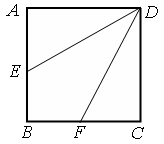

(1)求证: ;
;
(2)求二面角 的余弦值.
的余弦值.
已知数列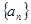 的前
的前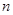 项和为
项和为 ,数列
,数列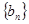 的首项
的首项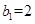 ,且点
,且点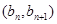 在直线
在直线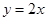 上.
上.
(1)求数列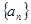 ,
,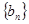 的通项公式;
的通项公式;
(2)若 ,求数列
,求数列 的前
的前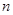 项和
项和 .
.
为了了解某班的男女生学习体育的情况,按照分层抽样分别抽取了10名男生和5名女生作为样本,他们期末体育成绩的茎叶图如图所示,其中茎为十位数,叶为个位数。
(Ⅰ)若该班男女生平均分数相等,求x的值;
(Ⅱ)若规定85分以上为优秀,在该10名男生中随机抽取2名,优秀的人数记为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
已知函数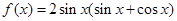 .
.
(Ⅰ)求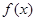 的最小正周期;
的最小正周期;
(Ⅱ)当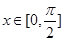 时,求
时,求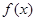 的最大值.
的最大值.