某班主任对班级22名学生进行了作业量多少的调查,数据如下:在喜欢玩电脑游戏的12中,有9人认为作业多,3人认为作业不多;在不喜欢玩电脑游戏的10人中,有4人认为作业多,6人认为作业不多.
(Ⅰ)根据以上数据建立一个 列联表;
列联表;
(Ⅱ)试问喜欢电脑游戏与认为作业多少是否有关系?
(可能用到的公式: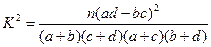 ,可能用到数据:
,可能用到数据: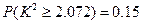 ,
,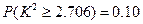 ,
,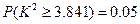 ,
,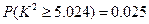 .)
.)
(本小题满分12分)贵广高速铁路自贵阳北站起,经黔南州、黔东南、广西桂林、贺州、广东肇庆、佛山终至广州南站. 其中广东省内有怀集站、广宁站、肇庆东站、三水南站、佛山西站、广州南站共6个站. 记者对广东省内的6个车站的外观进行了满意度调查,得分情况如下:
| 车站 |
怀集站 |
广宁站 |
肇庆东站 |
三水南站 |
佛山西站 |
广州南站 |
| 满意度得分 |
70 |
76 |
72 |
70 |
72 |
x |
已知6个站的平均得分为75分.
(1)求广州南站的满意度得分x,及这6个站满意度得分的标准差;
(2)从广东省内前5个站中,随机地选2个站,求恰有1个站得分在区间(68,75)中的概率.
(本小题满分12分)已知向量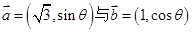 互相平行,其中
互相平行,其中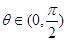 .
.
(1)求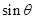 和
和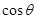 的值;
的值;
(2)求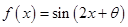 的最小正周期和单调递增区间.
的最小正周期和单调递增区间.
(本小题满分14分)已知函数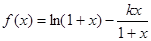 ,
, .
.
(1)讨论 的单调区间;
的单调区间;
(2)当 时,求
时,求 在
在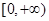 上的最小值,并证明
上的最小值,并证明 .
.
(本小题满分14分)若函数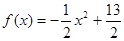 在区间 [a,b]上的最小值为2a,最大值为2b,求[a,b].
在区间 [a,b]上的最小值为2a,最大值为2b,求[a,b].
(本小题满分14分)已知在数列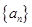 中,
中,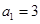 ,
, ,
,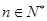 .
.
(1)证明数列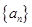 是等差数列,并求
是等差数列,并求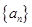 的通项公式;
的通项公式;
(2)设数列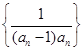 的前
的前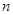 项和为
项和为 ,证明:
,证明: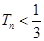 .
.