(本小题满分12分)
已知函数 为奇函数,
为奇函数, 为偶函数
为偶函数 ,且
,且 .
.
(1)求函数 的解析式;
的解析式;
(2)若存在 ,则称
,则称 是函数
是函数 的一个不动点,求函数
的一个不动点,求函数 的不动点
的不动点
.选修4—4:坐标系与参数方程
在极坐标系中,O为极点,已知圆C的圆心为 ,半径r=1,P在圆C上运动。
,半径r=1,P在圆C上运动。
(1)求圆C的极坐标方程;
(2)在直角坐标系(与极坐标系取相同的长度单位,且以极点O为原点,以极轴为x轴正半轴)中,若Q为线段OP的中点,求点Q轨迹的直角坐标方程。
.选修4-1:几何证明选讲
如图,已知 ,过顶点
,过顶点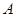 的圆与边
的圆与边 切于
切于 的中点
的中点 ,与边
,与边 分别交于点
分别交于点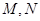 ,且
,且 ,点
,点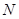 平分
平分 .求证:
.求证: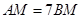 .
.
.(本小题满分12分)已知函数 的图象为曲线
的图象为曲线 , 函数
, 函数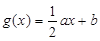 的图象为直线
的图象为直线 .
.
(1) 当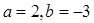 时, 求
时, 求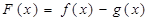 的最大值;
的最大值;
(2) 设直线  与 曲线
与 曲线 的交点的横坐标分别为
的交点的横坐标分别为 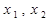 , 且
, 且  ,
,
求证:  .
.
.
设A(x1,y1),B(x2,y2),是椭圆 +
+ =(a>b>0)上的两点,已知向量m=(
=(a>b>0)上的两点,已知向量m=( ,
,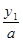 ),n=(
),n=( ,
, ),若m·n=0且椭圆的离心率e=
),若m·n=0且椭圆的离心率e= ,短轴长为2,O为坐标原点.
,短轴长为2,O为坐标原点.
(Ⅰ)求椭圆的方程;
(Ⅱ)试问:△AOB的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
..(本小题满分12分)如图,在直三棱柱ABC—A1B1C1D1中,点M是A1B的中点,点N是B1C的中点,连接MN。
(I)证明:MN//平面ABC;
(II)若AB=1, ,点P是CC1的中点,求四面体B1—APB的体积。
,点P是CC1的中点,求四面体B1—APB的体积。