(1)已知公差不为0的数列{an}的首项a1=1,前n项的和为Sn,若数列{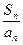 }是等差数列,
}是等差数列,
①求an;②令bn=qSn(q>0),若对一切n∈N*,都有 >2bn*bn+2,求q的取值范围。
>2bn*bn+2,求q的取值范围。
(2)是否存在各项都是正整数的无穷数列{cn},使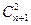 >2Cn*Cn+2对一切n∈N*都成立,若存在,请写出数列的一个通项公式,若不存在,说明理由。
>2Cn*Cn+2对一切n∈N*都成立,若存在,请写出数列的一个通项公式,若不存在,说明理由。
(本小题共13分)
已知数列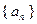 是首项为
是首项为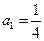 ,公比
,公比 的等比数列.设
的等比数列.设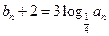
 ,数列
,数列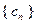 满足
满足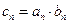 .
.
(Ⅰ)求证:数列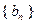 成等差数列;
成等差数列;
(Ⅱ)求数列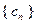 的前
的前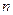 项和
项和 ;
;
(Ⅲ)若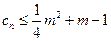 对一切正整数
对一切正整数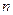 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题共14分)
已知椭圆的中心在坐标原点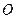 ,长轴长为
,长轴长为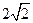 ,离心率
,离心率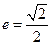 ,过右焦点
,过右焦点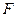 的直线
的直线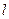 交椭圆于
交椭圆于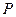 ,
,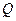 两点.
两点.
(Ⅰ)求椭圆的方程;
(Ⅱ)当直线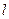 的斜率为1时,求
的斜率为1时,求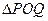 的面积;
的面积;
(Ⅲ)若以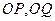 为邻边的平行四边形是矩形,求满足该条件的直线
为邻边的平行四边形是矩形,求满足该条件的直线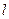 的方程.
的方程.
(本小题共14分)
已知函数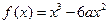 .
.
(Ⅰ)当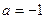 时,求曲线
时,求曲线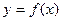 在点
在点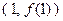 处的切线方程;
处的切线方程;
(Ⅱ)讨论函数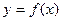 的单调性.
的单调性.
(本小题共13分)
某中学高中学生有900名,学校要从中选出9名同学作为国庆60周年庆祝活动的志愿者.已知高一有400名学生,高二有300名学生,高三有200名学生.为了保证每名同学都有参与的资格,学校采用分层抽样的方法抽取.
(Ⅰ)求高一、高二、高 三分别抽取学生的人数;
三分别抽取学生的人数;
(Ⅱ)若再从这9名同学中随机的抽取2人作为活动负责人,求抽到的这2名同学都是高一学生的概率;
(Ⅲ)在(Ⅱ)的条件下,求抽到的这2名同学不是同一年级的概率.
(本小题共14分)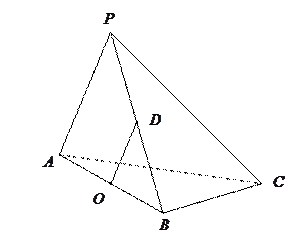
在三棱锥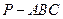 中,
中,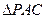 和
和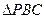 是边长为
是边长为 的等边三角形,
的等边三角形,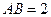 ,
,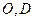 分别是
分别是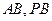 的中点.
的中点.
(Ⅰ)求证: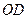 ∥平面
∥平面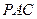 ;
;
(Ⅱ)求证:平面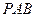 ⊥平面
⊥平面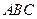 ;
;
(Ⅲ)求三棱锥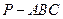 的体积.
的体积.