(本小题满分12 分)
分)
定义在 上的函数
上的函数 ,其中
,其中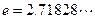 是自然对数的底数,
是自然对数的底数,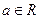 .
.
(1) 若函数 在点
在点 处连续,求
处连续,求 的值;
的值;
(2) 若函数 为
为 上的单调函数,求实
上的单调函数,求实 数
数 的取值范围,并判断此时函数
的取值范围,并判断此时函数 在
在 上是否为单调函数.
上是否为单调函数.
如图,在三棱 柱
柱 中,已知
中,已知
 ,
,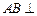 侧面
侧面
(1)求直线C1B与底面ABC所成角的正弦值;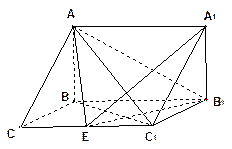
(2)在棱 (不包含端点
(不包含端点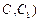 上确定一点
上确定一点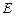 的位置,使得
的位置,使得 (要求说明理由).
(要求说明理由).
(3)在(2)的条件下,若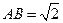 ,求二面角
,求二面角 的大小.
的大小.
(本小题满分13分)
已知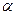 为锐角,且
为锐角,且 ,函数
,函数
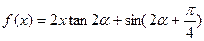 ,数列{
,数列{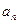 }的首项
}的首项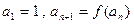 .
.
(1) 求函数 的表达式;
的表达式;
(2)在 中,若
中,若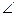 A=2
A=2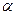 ,
,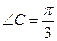 ,BC=2,求
,BC=2,求 的面积
的面积
(3) 求数列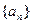 的前
的前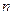 项和
项和
从装有2只红球,2只白球和1只黑球的袋中逐一取球,已知每只球被抽取的可能性相同。(1)若抽取后又放回,抽3次,
①分别求恰2次为红球的概率及抽全三种颜色球的概率;
②求抽到红球次数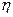 的数学期望
的数学期望
(2)若抽取后不放回,抽完红球所需次数为 的分布列及期望。
的分布列及期望。
已知抛物线C:x =2py(
=2py( p>0)上一点A(m,4)到其焦点的距离为
p>0)上一点A(m,4)到其焦点的距离为 .
.
(Ⅰ)求p和m的值;
(Ⅱ)设B(-1,1),过点B任作两直线A1B1,A2B2,与抛物线C分别交于点A1,B1,A2,B2,过A1,B1的抛物线C的两切线交于P,过A2,B2的抛物线C的两切线交于Q,求PQ的直线方程.
已知函数 且
且
(Ⅰ)若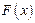 在
在 取得极小值-2,求函数
取得极小值-2,求函数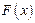 的单调区间.
的单调区间.
(Ⅱ)令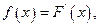 若
若 的解集为A,且
的解集为A,且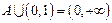 ,求
,求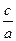 的取值范围.
的取值范围.