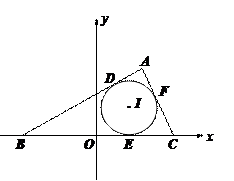
本小题满分12分 的内切圆与三边
的内切圆与三边 的切点分别为
的切点分别为 ,已知
,已知 ,内切圆圆心
,内切圆圆心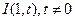 ,设点
,设点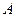 的轨迹为
的轨迹为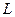 .
.
(1)求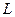 的方程;
的方程;
(2)过点 的动直线
的动直线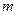 交曲线
交曲线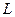 于不同的两点
于不同的两点 (点
(点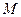 在
在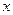 轴的上方),问在
轴的上方),问在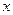 轴上是否存在一定点
轴上是否存在一定点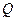 (
(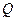 不与
不与 重合),使
重合),使 恒成立,若存在,试求出
恒成立,若存在,试求出 点的坐标;若不存在,说明理由.
点的坐标;若不存在,说明理由.
(本小题满分12分)
在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2.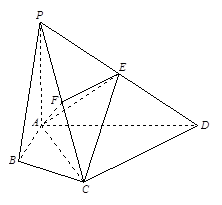
(Ⅰ)求四棱锥P-ABCD的体积V;
(Ⅱ)若F为PC的中点,求证PC⊥平面AEF;
(本小题满分12分)
有两枚大小相同、质地均匀的正四面体玩具,每个玩具的各个面上分别写着数字1,2,3,5.同时投掷这两枚玩具一次,记 为两个朝下的面上的数字之和.
为两个朝下的面上的数字之和.
(Ⅰ)求事件“m不小于6”的概率;
(Ⅱ)“m为奇数”的概率和“m为偶数”的概率是不是相等?证明你作出的结论.
(本小题满分12分)
已知等比数列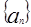 中,
中, ,公比
,公比 .
.
(I) 为
为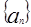 的前
的前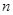 项和,证明:
项和,证明:
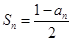
(II)设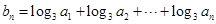 ,求数列
,求数列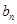 的通项公式.
的通项公式.
(本小题满分14分)
已知函数
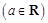 .
.
(Ⅰ)当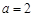 时,求函数
时,求函数 的图象在
的图象在 处的切线方程;
处的切线方程;
(Ⅱ)判断函数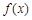 的单调性;
的单调性;
(Ⅲ)若函数 在
在 上为增函数,求
上为增函数,求 的取值范围.
的取值范围.
(本小题满分12分)
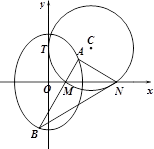
如图,圆 与
与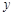 轴相切于点
轴相切于点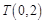 ,与
,与 轴正半轴相交于两点
轴正半轴相交于两点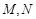 (点
(点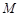 在点
在点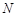 的左侧),且
的左侧),且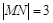 .
.
(Ⅰ)求圆 的方程;
的方程;
(Ⅱ)过点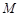 任作一条直线与椭圆
任作一条直线与椭圆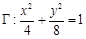 相交于
相交于 两点,连接
两点,连接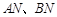 ,求证:
,求证: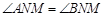 .
.