(、如图,在底面是直角梯形的四棱锥S-AB CD中,
CD中,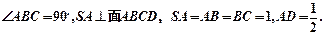

(1)求四棱锥S-ABCD的体积;
(2)求证: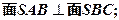
某上市股票在30天内每股的交易价格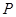 (元)与时间
(元)与时间 (天)所组成的有序数对
(天)所组成的有序数对 落在下图中的两条线段上,该股票在30天内的日交易量
落在下图中的两条线段上,该股票在30天内的日交易量 (万股)与时间
(万股)与时间 (天)的部分数据如下表所示.
(天)的部分数据如下表所示.
| 第t天 |
4 |
10 |
16 |
22 |
| Q(万股) |
36 |
30 |
24 |
18 |
⑴根据提供的图象,写出该种股票每股交易价格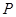 (元)与时间
(元)与时间 (天)所满足的函数关系式;
(天)所满足的函数关系式;
⑵根据表中数据确定日交易量 (万股)与时间
(万股)与时间 (天)的一次函数关系式;
(天)的一次函数关系式;
⑶在(2)的结论下,用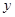 (万元)表示该股票日交易额,写出
(万元)表示该股票日交易额,写出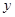 关于
关于 的函数关系式,并求这30天中第几天日交易额最大,最大值为多少?
的函数关系式,并求这30天中第几天日交易额最大,最大值为多少?
在函数 的图象上有
的图象上有 、
、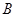 、
、 三点,横坐标分别为
三点,横坐标分别为 其中
其中 .
.
⑴求 的面积
的面积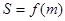 的表达式;
的表达式;
⑵求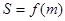 的值域.
的值域.
设命题 :函数
:函数 在
在 上单调递减,命题
上单调递减,命题 :不等式
:不等式 的解集为
的解集为 ,若
,若 为真,
为真, 为假,求实数
为假,求实数 的取值范围.
的取值范围.
已知 ,若
,若 ,且
,且 ,求
,求 、
、 的值.
的值.
P(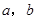 )是平面上的一个点,设事件A表示“
)是平面上的一个点,设事件A表示“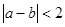 ”,其中
”,其中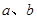 为实常数.
为实常数.
(1)若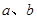 均为从0,1,2,3,4五个数中任取的一个数,求事件A发生的概率;
均为从0,1,2,3,4五个数中任取的一个数,求事件A发生的概率;
(2)若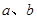 均为从区间[0,5)任取的一个数,求事件A发生的概率.
均为从区间[0,5)任取的一个数,求事件A发生的概率.