（ 为赢得2010年广州亚运会的商机，某商家最近进行了新科技产品的市场分析，调查显示，新产品每件成本9万元，售价为30万元，每星期卖出432件，如果降低价格，销售量可以增加，且每星期多卖出的商品件数与商品单价的降低值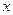
（单位：万元，
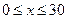）的平方成正比，已知商品单价降低2万元时，一星期多卖出24件．（1）将一个星期的商品销售利润表示成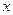的函数；
（2）如何定价才能使一个星期的商品销售利润最大？
已知函数
（1）若
为奇函数，求实数
的值；
（2）当
时，求函数
在
上的值域；
（3）若
对
恒成立，求实数的取值范围．
在
中，角
的对边分别是
，若
（1）求角
；
（2）若
，
，求的面积
．
甲、乙两位学生参加数学竞赛培训，他们在培训期间8次模拟考试的成绩如下：
甲：82 81 79 78 95 88 93 84
乙：92 95 80 75 83 80 90 85
画出甲、乙两位学生成绩的茎叶图，求学生甲的中位数
（2）并求学生乙成绩的平均数和方差；
（3）从甲同学超过80分的6个成绩中任取两个，求这两个成绩中至少有一个超过90分的概率．
如图，在四棱锥
中，平面
平面
，
∥
是正三角形，已知
（1）设
是
上的一点，求证:平面
平面
；
（2）求四棱锥的体积．
已知公差不为0的等差数列
的前
项和为
，若
，且
成等比数列
（1）求的通项公式；
（2）设
，求数列
的前项和为
．