甲、乙两位学生参加数学竞赛培训,他们在培训期间8次模拟考试的成绩如下:
甲:82 81 79 78 95 88 93 84
乙:92 95 80 75 83 80 90 85
画出甲、乙两位学生成绩的茎叶图,求学生甲的中位数
(2)并求学生乙成绩的平均数和方差;
(3)从甲同学超过80分的6个成绩中任取两个,求这两个成绩中至少有一个超过90分的概率.
已知函数 ,
,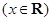 .
.
(1)证明:函数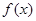 在区间
在区间 上为增函数,并指出函数
上为增函数,并指出函数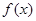 在区间
在区间 上的单调性.
上的单调性.
(2)若函数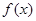 的图像与直线
的图像与直线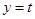 有两个不同的交点
有两个不同的交点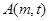 ,
, ,其中
,其中 ,求
,求 关于
关于 的函数关系式.
的函数关系式.
(3)求 的取值范围.
的取值范围.
已知数列 为等差数列,公差
为等差数列,公差 ,且
,且
(1)求证:当k取不同自然数时,此方程有公共根;
(2)若方程不同的根依次为 …,求证:数列
…,求证:数列 为等差数列.
为等差数列.
已知
(1)求 的值;
的值;
(2)求 的值.
的值.
如图:三棱锥 中,
中, ^底面
^底面 ,若底面
,若底面 是边长为2的正三角形,且
是边长为2的正三角形,且 与底面
与底面 所成的角为
所成的角为 .若
.若 是
是 的中点,求:
的中点,求:
(1)三棱锥 的体积;
的体积;
(2)异面直线 与
与 所成角的大小(结果用反三角函数值表示).
所成角的大小(结果用反三角函数值表示).
已知数列 满足
满足
(1)设 是公差为
是公差为 的等差数列.当
的等差数列.当 时,求
时,求 的值;
的值;
(2)设 求正整数
求正整数 使得一切
使得一切 均有
均有
(3)设 当
当 时,求数列
时,求数列 的通项公式.
的通项公式.