(本小题满分12分)
已知函数f(x)=x2-ax+b (a,b∈R)的图像经过坐标原点,且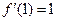 ,数列{
,数列{ }的前n项和
}的前n项和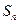 =f(n)(n∈N*).
=f(n)(n∈N*).
(Ⅰ) 求数列{ }的通项公式;(Ⅱ)若数列{
}的通项公式;(Ⅱ)若数列{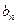 }满足
}满足 +
+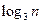 =
=  ,求数列{
,求数列{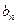 }的前n项和.
}的前n项和.
在平面 内,不等式
内,不等式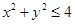 确定的平面区域为
确定的平面区域为 ,不等式组
,不等式组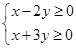 确定的平面区域为
确定的平面区域为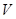 .
.
(1)定义横、纵坐标为整数的点为“整点”. 在区域 中任取3个“整点”,求这些“整点”中恰好有2个“整点”落在区域
中任取3个“整点”,求这些“整点”中恰好有2个“整点”落在区域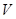 中的概率;
中的概率;
(2)在区域 中每次任取一个点,连续取3次,得到3个点,记这3个点落在区域
中每次任取一个点,连续取3次,得到3个点,记这3个点落在区域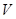 中的个数为
中的个数为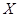 ,求
,求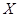 的分布列和数学期望.
的分布列和数学期望.
如图,在梯形△ABCD中,AB//CD,AD=DC-=CB=1, ABC=60。,四边形ACFE为矩形,平面ACFE上平面ABCD,CF=1.
ABC=60。,四边形ACFE为矩形,平面ACFE上平面ABCD,CF=1.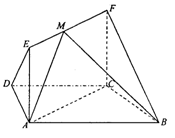
(1)求证:BC⊥平面ACFE;
(2)若M为线段EF的中点,设平面MAB与平面FCB所成角为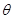 ,求
,求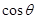 .
.
在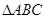 中,
中,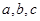 分别是角
分别是角 的对边,
的对边,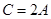 ,
, .
.
(1)求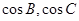 的值;
的值;
(2)若 ,求边
,求边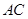 的长.
的长.
设数列 的前
的前 项和为
项和为 ,满足
,满足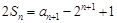 ,
,
 ,且
,且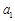 ,
,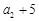 ,
,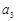 成等差数列.
成等差数列.
(1)求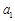 ,
, 的值;
的值;
(2) 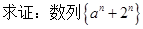 是等比数列
是等比数列
(3)证明:对一切正整数 ,有
,有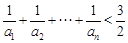 .
.
已知 .
.
(1)求函数 在
在 上的最小值;
上的最小值;
(2)对一切 恒成立,求实数
恒成立,求实数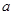 的取值范围;
的取值范围;
(3)证明:对一切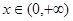 ,都有
,都有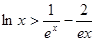 成立.
成立.