在平面 内,不等式
内,不等式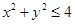 确定的平面区域为
确定的平面区域为 ,不等式组
,不等式组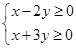 确定的平面区域为
确定的平面区域为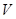 .
.
(1)定义横、纵坐标为整数的点为“整点”. 在区域 中任取3个“整点”,求这些“整点”中恰好有2个“整点”落在区域
中任取3个“整点”,求这些“整点”中恰好有2个“整点”落在区域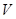 中的概率;
中的概率;
(2)在区域 中每次任取一个点,连续取3次,得到3个点,记这3个点落在区域
中每次任取一个点,连续取3次,得到3个点,记这3个点落在区域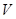 中的个数为
中的个数为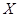 ,求
,求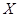 的分布列和数学期望.
的分布列和数学期望.
已知函数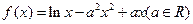 .
.
(Ⅰ)当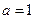 时,证明函数
时,证明函数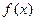 只有一个零点;
只有一个零点;
(Ⅱ)若函数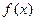 在区间
在区间 上是减函数,求实数
上是减函数,求实数 的取值范围.
的取值范围.
已知函数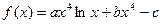
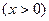 在
在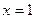 处取得极值
处取得极值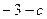 ,其中
,其中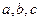 为常数.
为常数.
(1)求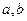 的值;
的值;
(2)求函数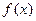 的单调区间;
的单调区间;
(3)若对任意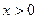 ,不等式
,不等式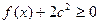 恒成立,求
恒成立,求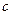 的取值范围.
的取值范围.
设在一个盒子中,放有标号分别为1,2,3的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片,标号分别记为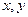 ,设随机变量
,设随机变量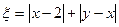 .
.
(1)写出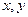 的可能取值,并求随机变量
的可能取值,并求随机变量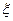 的最大值;
的最大值;
(2)求事件“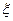 取得最大值”的概率;
取得最大值”的概率;
(3)求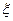 的分布列和数学期望与方差.
的分布列和数学期望与方差.
某家具城进行促销活动,促销方案是:顾客每消费满1000元,便可以获得奖券一张,每张奖券
中奖的概率为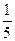 ,若中奖,则家具城返还顾客现金1000元,某顾客购买一张价格为3400元的餐桌,
,若中奖,则家具城返还顾客现金1000元,某顾客购买一张价格为3400元的餐桌,
得到3张奖券,设该顾客购买餐桌的实际支出为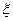 元;
元;
(I)求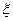 的所有可能取值;
的所有可能取值;
(II)求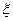 的分布列;
的分布列;
(III)求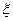 的期望E(
的期望E(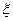 );
);
过点A(6,4)作曲线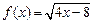 的切线l.
的切线l.
(1)求切线l的方程;
(2)求切线l,x轴及曲线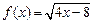 所围成的封闭图形的面积S.
所围成的封闭图形的面积S.