已知a,b,c为正数,且满足abc=1.证明:
(1) ;
(2) .
为了参加 贵州省高中篮球比赛,某中学决定从四个篮球较强的班级的篮球队员中选出
贵州省高中篮球比赛,某中学决定从四个篮球较强的班级的篮球队员中选出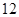 人组成男子篮球队,代表该地区参赛,四个篮球较强的班级篮球队员人数如下表:
人组成男子篮球队,代表该地区参赛,四个篮球较强的班级篮球队员人数如下表:
| 班级 |
高三(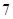 )班 )班 |
高三(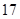 )班 )班 |
高二( )班 )班 |
高二( )班 )班 |
| 人数 |
12 |
6 |
9 |
9 |
(Ⅰ)现采取分层抽样的方法从这四个班中抽取运动员,求应分别从这四个班抽出的队员人数;
(Ⅱ)该中学篮球队奋力拼搏,获得冠军.若要从高三年级抽出的队员中选出两位队员作为冠军的代表发言,求选出的两名队员来自同一班的概率.
已知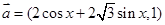 ,
, ,且
,且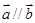 .
.
(I)将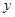 表示成
表示成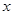 的函数
的函数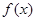 ,并求
,并求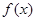 的最小正周期;
的最小正周期;
(II)记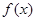 的最大值为
的最大值为 ,
, 、
、 、
、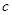 分别为
分别为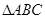 的三个内角
的三个内角 、
、 、
、 对应的边长,若
对应的边长,若 且
且 ,求
,求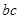 的最大值.
的最大值.
已知函数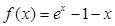
(Ⅰ)求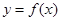 在点
在点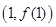 处的切线方程;
处的切线方程;
(Ⅱ)若存在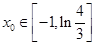 ,满足
,满足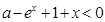 成立,求
成立,求 的取值范围;
的取值范围;
(Ⅲ)当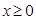 时,
时, 恒成立,求
恒成立,求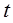 的取值范围.
的取值范围.
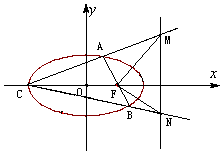
设椭圆C: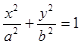
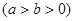 过点
过点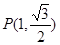 , 且离心率
, 且离心率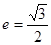 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过右焦点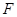 的动直线交椭圆于点
的动直线交椭圆于点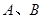 ,设椭圆的左顶点为
,设椭圆的左顶点为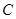 连接
连接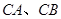 且交动直线
且交动直线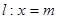 于
于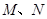 ,若以MN为直径的圆恒过右焦点F,求
,若以MN为直径的圆恒过右焦点F,求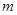 的值.
的值.
2011年4月28日世界园艺博览会将在陕西西安浐灞生态区举行,为了接待来自国内外的各界人士,需招募一批志愿者,要求志愿者不仅要有一定的气质,还需有丰富的人文、地理、历史等文化知识。志愿者的选拔分面试和知识问答两场,先是面试,面试通过后每人积60分,然后进入知识问答。知识问答有A,B,C,D四个题目,答题者必须按A,B,C,D顺序依次进行,答对A,B,C,D四题分别得20分、20分、40分、60分,每答错一道题扣20分,总得分在面试60分的基础上加或减。答题时每人总分达到100分或100分以上,直接录用不再继续答题;当四道题答完总分不足100分时不予录用。
假设志愿者甲面试已通过且第二轮对A,B,C,D四个题回答正确的概率依次是 ,且各题回答正确与否相互之间没有影响.
,且各题回答正确与否相互之间没有影响.
(Ⅰ) 用X表示志愿者甲在知识问答结束时答题的个数,求X的分布列和数学期望;
(Ⅱ)求志愿者甲能被录用的概率.