(本小题满分12分)
如图: 正在海上A处执行任务的渔政船甲和在B处执行任务的渔政船乙,同时收到同一片海域上一艘渔船丙的求救信号,此时渔船丙在渔政船甲的南偏东40°方向距渔政船甲70km的C处,渔政船乙在渔政船甲的南偏西20°方向的B处,两艘渔政船协调后立即让
正在海上A处执行任务的渔政船甲和在B处执行任务的渔政船乙,同时收到同一片海域上一艘渔船丙的求救信号,此时渔船丙在渔政船甲的南偏东40°方向距渔政船甲70km的C处,渔政船乙在渔政船甲的南偏西20°方向的B处,两艘渔政船协调后立即让 渔政船甲向渔船丙所在的位置C处沿直线AC航行前去救援,渔政船乙仍留在B处执行任务,渔政船甲航行30km到达D处时,收到新的指令另有重要任务必须执行,于是立即通知在B处执行任务的渔政船乙前去救援渔船丙(渔政船乙沿直线BC航行前去救援渔船丙),此时B、D两处相距42km,问渔政船乙要航行多少距离才能到达渔船丙所在的位置C处实施营救.
渔政船甲向渔船丙所在的位置C处沿直线AC航行前去救援,渔政船乙仍留在B处执行任务,渔政船甲航行30km到达D处时,收到新的指令另有重要任务必须执行,于是立即通知在B处执行任务的渔政船乙前去救援渔船丙(渔政船乙沿直线BC航行前去救援渔船丙),此时B、D两处相距42km,问渔政船乙要航行多少距离才能到达渔船丙所在的位置C处实施营救.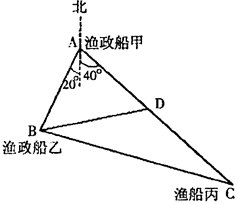
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB= ,PD⊥平面ABCD,AD=1,点
,PD⊥平面ABCD,AD=1,点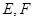 分别为为AB和PD中点.
分别为为AB和PD中点.
(Ⅰ)求证:直线AF 平面PEC ;
平面PEC ;
(Ⅱ)若直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 ,求
,求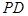 的长..
的长..
已知函数 的图象过点
的图象过点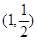 ,且点
,且点
 在函数
在函数 的图象上.
的图象上.
(1)求数列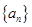 的通项公式;
的通项公式;
(2)令 ,若数列的前
,若数列的前 项和为
项和为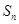 ,求证:
,求证: .
.
选修4-5:不等式选讲
已知函数 .
.
(1)当 时,解不等式
时,解不等式 ;
;
(2)若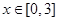 时,
时, ,求
,求 的取值范围.
的取值范围.
已知曲线 的参数方程为
的参数方程为 为参数,
为参数, ),直线
),直线 在参数方程是
在参数方程是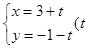 为参数),曲线
为参数),曲线 与直线
与直线 有一个公共点在
有一个公共点在 轴上,以坐标原点为极点,
轴上,以坐标原点为极点, 轴的正半轴为极轴建立极坐标系。
轴的正半轴为极轴建立极坐标系。
(1)求曲线 的普通方程;
的普通方程;
(2)若点 在曲线
在曲线 上,求
上,求 的值。
的值。
如图, 是直角三角形,
是直角三角形, .以
.以 为直径的圆
为直径的圆 交
交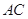 于点
于点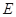 ,点
,点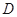 是
是 边的中点.连结
边的中点.连结 交圆
交圆 于点
于点 .
.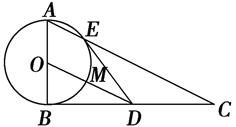
(Ⅰ)求证: 、
、 、
、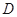 、
、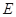 四点共圆;
四点共圆;
(Ⅱ )求证: