(本小题满分16分)
如图,实线部分的月牙形公园是由圆P上的一段优弧和圆Q上的一段劣弧围成,圆P和圆Q的半径都是2km,点P在圆Q上,现 要在公园内建一块顶点都在圆P上的多边形活动场地.
要在公园内建一块顶点都在圆P上的多边形活动场地.
(1)如图甲,要建的活动场地为△RST,求场地的最大面积;
(2)如图乙,要建的活动场地为等腰梯形ABCD,求场地的最大面积.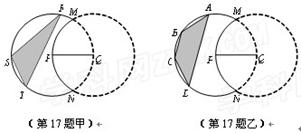
已知 中,
中, 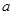 ,
,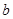 ,
, 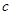 分别为角
分别为角  ,
, ,
, 所对的边,
所对的边, .
.
(Ⅰ)求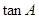 的值;
的值;
(Ⅱ)若 的面积为
的面积为 ,
,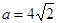 ,求
,求 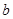 、
、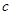 的长.
的长.
(本小题满分14分)已知函数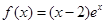 和
和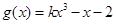 .
.
(Ⅰ)若函数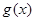 在区间
在区间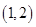 不单调,求实数
不单调,求实数 的取值范围;
的取值范围;
(Ⅱ)当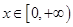 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的最大值.
的最大值.
(本小题满分15分)已知椭圆 的左右焦点
的左右焦点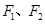 ,离心率为
,离心率为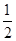 ,双曲线方程为
,双曲线方程为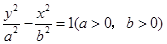 ,直线
,直线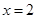 与双曲线的交点为
与双曲线的交点为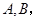 且
且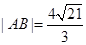 .
.
(Ⅰ)求椭圆与双曲线的方程;
(Ⅱ)过点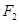 的直线
的直线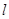 与椭圆交于
与椭圆交于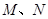 两点,交双曲线与
两点,交双曲线与 两点,当
两点,当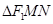 (
( 为椭圆的左焦点)的内切圆的面积取最大值时,求
为椭圆的左焦点)的内切圆的面积取最大值时,求 的面积.
的面积.
(本小题满分15分)如图,在三棱锥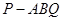 中,
中,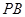 ⊥平面
⊥平面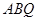 ,
,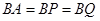 ,
, ,
,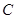 ,
,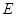 ,
, 分别是
分别是 ,
,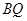 ,
,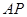 ,
, 的中点,
的中点, ,
,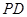 与
与 交于点
交于点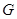 ,
, 与
与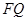 交于点
交于点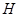 ,连结
,连结 .
.
(Ⅰ)求证: ;
;
(Ⅱ)求平面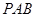 与平面
与平面 所成角的正弦值.
所成角的正弦值.
(本小题满分14分)设数列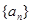 的前
的前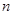 项和为
项和为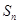 ,点
,点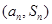 在直线
在直线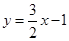 上.
上.
(Ⅰ)求数列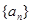 的通项公式;
的通项公式;
(Ⅱ)在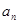 与
与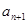 之间插入
之间插入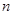 个数,使这
个数,使这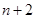 个数组成公差为
个数组成公差为 的等差数列,求数列
的等差数列,求数列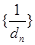 的前
的前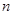 项和
项和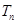 ,并求使
,并求使 成立的正整数
成立的正整数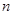 的最大值.
的最大值.