(本小题满分16分)
已知数列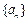
满足
．
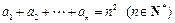（1）求数列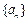的通项公式；
（2）对任意给定的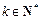
，是否存在
（
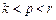）使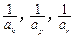
成等差数列？若存在，用
分别表示
和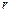
（只要写出一组）；若不存在，请说明理由；
（3）证明：存在无穷多个三边成等比数列且互不相似的三角形，其边长为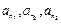
．
对某校高二年级学生参加社区服务次数进行统计，随机抽取M名学生作为样本，得到这M名学生参加社区服务的次数根据此数据作出了频数与频率的统计表和频率分布直方图如下：
（1）求出表中M，p及图中a的值；
（2）在所取样本中，从参加社区服务的次数不少于20次的学生中任选2人，求至多一人参加社区服务次数在区间
内的概率
已知函数
的图象的两条相邻对称轴间的距离等于
，在
ABC中，角A，B，C所对的边依次为a，b，c，若
， b+c=3，
，求ABC的面积．
己知长方体的三条棱长分别为a、b、c，其外接球的半径为
（1）求长方体体积的最大值：
（2）设
，求
的最大值
己知抛物线
的顶点M到直线
(t为参数)的距离为1
（1）求m；
（2）若直线
与抛物线相交于A，B两点，与y轴交于N点，求
的值．
（本小题满分10分）选修4-l：几何证明选讲如图，
是
ABC的外接圆，D是
的中点，BD 交AC于E
（1）求证：
：
（2）若
，O到AC的距离为1，求的半径