某次运动会甲、乙两名射击运动员成绩如下:
甲:9.4,8.7,7.5,8.4,10.1,10.5,10.7,7.2,7.8,10.8;
乙:9.1,8.7,7.1,9.8,9.7,8.5,10.1,9.2,10.1,9.1;
(1)用茎叶图表示甲,乙两个成绩;
(2)分别计算两个样本的平均数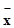 和标准差s,并根据计算结果估计哪位运动员的成绩比较稳定.
和标准差s,并根据计算结果估计哪位运动员的成绩比较稳定.
如图1,给出了一个程序框图,其作用是输入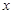 的值,输出相应的
的值,输出相应的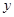 的值,
的值,
(I)请指出该程序框图所使用的逻辑结构;
(Ⅱ)若视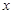 为自变量,
为自变量,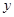 为函数值,试写出函数
为函数值,试写出函数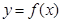 的解析 式;
的解析 式;
(Ⅲ)若要使输入的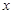 的值与输出的
的值与输出的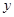 的值相等,则输入
的值相等,则输入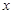 的值的集合是什么?
的值的集合是什么?
青少年“心理健康”问题越来越引起社会关注,某校对高一600名学生进行了一次“心理健康”知识测试,并从中抽取了部分学生的成绩(满分100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.
(1)填写答题卡频率分布表中的空格,补全频率分布直方图,并标出每个小矩形对应的纵轴数据;
(2)试估计该年段成绩在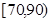 段的有多少人;
段的有多少人;
(3)请你估算该年段的平均分.
(1)已知角θ的终边上一点P(x,3) (x≠0),且cos θ= x,求sin θ,tan θ.
x,求sin θ,tan θ.
( 2)已知 ,求
,求 的值.
的值.
某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如图所示(在答题卡上).
(Ⅰ)请先求出频率分布表中①、②位置相应的数据,再在答题纸上完成下列频率分布直方图;
(Ⅱ)为了能选拔出最优秀的学生,该高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(Ⅲ)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官的面试,求第四组至少有一名学生被考官A面试的概率?