已知数列{an}中，a1＝1，an＋1＝
(n∈N*)．
(1)求证： 数列 ｛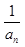
＋
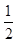｝是等比数列，并求数列{an}的通项an
(2)若数列{bn}满足bn＝(3n－1)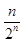
an，数列{bn}的前n项和为Tn，若不等式(－1)nλ＜Tn对一切n∈N*恒成立，求λ的取值范围．
已知关于x的不等式：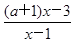
<1.
(1)当a＝1时，解该不等式；
(2)当a为任意实数时，解该不等式．
在公差为d的等差数列{an}中，已知a1＝10，且a1,2a2＋2,5a3成等比数列．
(1)求d，an；
(2)若d＜0，求|a1|＋|a2|＋|a3|＋…＋|an|.
如图，半圆O的直径为2，A为直径延长线上的一点，OA＝2，B为半圆上任意一点，以AB为一边作等边三角形ABC.问：点B在什么位置时，四边形OACB面积最大？
已知直线L：kx－y＋1＋2k＝0.
(1)求证：直线L过定点；
(2)若直线L交x轴负半轴于点A，交y正半轴于点B，△AOB的面积为S，试求S的最小值并求出此时直线L的方程．
中，
，
，记
，
.
是等比数列；
，数列
的前n项和为
，求证：
．