已知数列{an}中,a1=1,an+1= (n∈N*).
(n∈N*).
(1)求证: 数列 {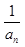 +
+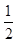 }是等比数列,并求数列{an}的通项an
}是等比数列,并求数列{an}的通项an
(2)若数列{bn}满足bn=(3n-1)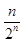 an,数列{bn}的前n项和为Tn,若不等式(-1)nλ<Tn对一切n∈N*恒成立,求λ的取值范围.
an,数列{bn}的前n项和为Tn,若不等式(-1)nλ<Tn对一切n∈N*恒成立,求λ的取值范围.
选修4-4:坐标系与参数方程选讲. 在极坐标系中, O为极点, 半径为2的圆C的圆心的极坐标为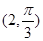 .
.
(1)求圆C的极坐标方程;
(2)在以极点O为原点,以极轴为x轴正半轴建立的直角坐标系中,直线 的参数方程为
的参数方程为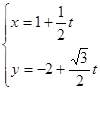 (t为参数),直线
(t为参数),直线 与圆C相交于A,B两点,已知定点
与圆C相交于A,B两点,已知定点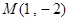 ,求|MA|·|MB|。
,求|MA|·|MB|。
选修4-1:几何证明选讲.如图, 是⊙
是⊙ 的直径,
的直径, 是⊙
是⊙ 的切线,
的切线, 与
与 的延长线交于点
的延长线交于点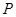 ,
, 为切点.若
为切点.若 ,
,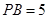 ,
,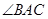 的平分线
的平分线 与
与 和⊙
和⊙ 分别交于点
分别交于点 、
、 ,求
,求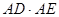 的值。
的值。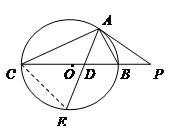
设函数
(1)若关于x的不等式 在
在 有实数解,求实数m的取值范围;
有实数解,求实数m的取值范围;
(2)设 ,若关于x的方程
,若关于x的方程 至少有一个解,求p 的最小值.
至少有一个解,求p 的最小值.
(3)证明不等式:

已知方向向量为 的直线l过椭圆
的直线l过椭圆 的焦点以及点(0,
的焦点以及点(0, ),直线l与椭圆C交于 A 、B两点,且A、B两点与另一焦点围成的三角形周长为
),直线l与椭圆C交于 A 、B两点,且A、B两点与另一焦点围成的三角形周长为 。
。
(1)求椭圆C的方程
(2)过左焦点 且不与x轴垂直的直线m交椭圆于M、N两点,
且不与x轴垂直的直线m交椭圆于M、N两点, (O坐标原点),求直线m的方程
(O坐标原点),求直线m的方程
如图,四棱锥 中,底面
中,底面 为平行四边形,
为平行四边形, ,
, ,
, ⊥底面
⊥底面 .
.
(1)证明:平面 平面
平面 ;
;
(2)若二面角 为
为 ,求
,求 与平面
与平面 所成角的正弦值。
所成角的正弦值。