(本小题满分15分)
在平面直角坐标 系中,已知点
系中,已知点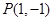 ,过点
,过点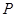 作抛物线
作抛物线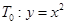 的切线,其切点分别为
的切线,其切点分别为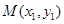 、
、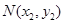 (其中
(其中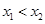 ).
).
(1)求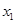 与
与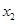 的值;
的值;
(2)若以点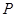 为圆心的圆
为圆心的圆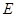 与直线
与直线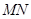 相切,求圆
相切,求圆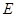 的面积;
的面积;
(3 )过原点
)过原点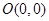 作圆
作圆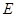 的两条互相垂直的弦
的两条互相垂直的弦 ,求四边形
,求四边形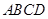 面积的最大值.
面积的最大值.
(本小题满分15分) 已知函数 ,
, ,其中
,其中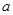 为实数.
为实数.
(1)设 为常数,求函数
为常数,求函数 在区间
在区间 上的最小值;
上的最小值;
(2) 若对一切
若对一切 ,不等式
,不等式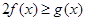 恒成立,求实数
恒成立,求实数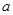 的取值范围.
的取值范围.
(本小题满分14分)如图,在一个由矩形 与正三角形
与正三角形 组合而成的平面图形中,
组合而成的平面图形中, 现将正三角形
现将正三角形 沿
沿 折成四棱锥
折成四棱锥 ,使
,使 在平面
在平面 内的射影恰好在边
内的射影恰好在边 上.
上. 
(1)求证:平面 ⊥平面
⊥平面 ;
;
(2)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
(本小题满分14分)已知等差数列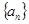 的公差为
的公差为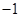 , 且
, 且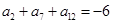 ,
,
(1)求数列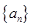 的通项公式
的通项公式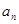 与前
与前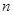 项和
项和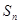 ;
;
(2)将数列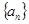 的前
的前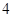 项抽去其中一项后,剩下三项按原来顺序恰为等比数列
项抽去其中一项后,剩下三项按原来顺序恰为等比数列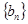 的前3项,记
的前3项,记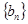 的前
的前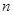 项和为
项和为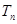 , 若存在
, 若存在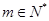 , 使对任意
, 使对任意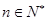 总有
总有 恒成立, 求实数
恒成立, 求实数 的取值范围.
的取值范围.
(本小题满分14分)在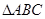 中,角
中,角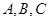 所对的边分别为
所对的边分别为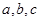 ,且
,且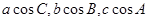 成等差数列.
成等差数列.
(1)求角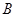 的大小;
的大小;
(2)若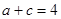 ,求
,求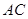 边上中线长的最小值.
边上中线长的最小值.