(本小题满分12分)
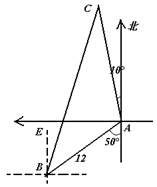
我缉私巡逻艇在一小岛A南偏西50º的方向,距小岛12海里的B处,发现隐藏在小岛边上的一走私船正开始向岛北偏西 10º方向行驶,测得其速度为每小时10海里,问我巡逻艇须用多大的速度朝什么方向航行才能恰在两小时后截获该走私船?(必要时,可参考下列数据sin38º≈0.62,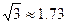 )
)
设等比数列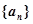 的首项为
的首项为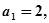 公比为
公比为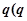 为正整数),且满足
为正整数),且满足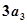 是
是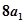 与
与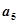 的等差中项;数列
的等差中项;数列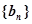 满足
满足 (1)求数列
(1)求数列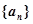 的通项公式;(2)试确定
的通项公式;(2)试确定 的值,使得数列
的值,使得数列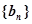 为等差数列.
为等差数列.
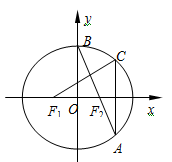
如图,在平面直角坐标系 中,
中, 分别是椭圆
分别是椭圆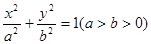 的左、右焦点,顶点
的左、右焦点,顶点 的坐标为
的坐标为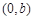 ,连结
,连结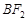 并延长交椭圆于点A,过点A作
并延长交椭圆于点A,过点A作 轴的垂线交椭圆于另一点C,连结
轴的垂线交椭圆于另一点C,连结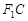 .
.
(1)若点C的坐标为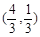 ,且
,且 ,求椭圆的方程;
,求椭圆的方程;
(2)若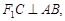 求椭圆离心率e的值.
求椭圆离心率e的值.
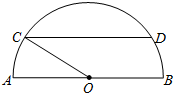
如图是一个半圆形湖面景点的平面示意图.已知 为直径,且
为直径,且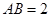 km,
km,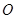 为圆心,
为圆心,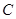 为圆周上靠近
为圆周上靠近 的一点,
的一点,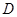 为圆周上靠近
为圆周上靠近 的一点,且
的一点,且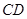 ∥
∥ .现在准备从
.现在准备从 经过
经过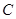 到
到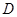 建造一条观光路线,其中
建造一条观光路线,其中 到
到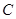 是圆弧
是圆弧 ,
,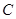 到
到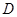 是线段
是线段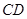 .设
.设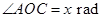 ,观光路线总长为
,观光路线总长为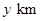 .
.
(1)求 关于
关于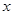 的函数解析式,并指出该函数的定义域;
的函数解析式,并指出该函数的定义域;
(2)求观光路线总长的最大值.
如图,在四棱锥 中,底面
中,底面 是菱形,且
是菱形,且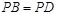 .
.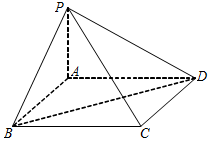
(1)求证: ;
;
(2)若平面 与平面
与平面 的交线为
的交线为 ,求证:
,求证: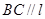 .
.
已知 的内角
的内角 的对边分别为
的对边分别为 ,
, .
.
(1)若 ,
,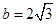 ,求
,求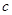 的值;
的值;
(2)若 ,求
,求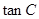 的值.
的值.