设 为直线
为直线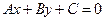 上一点,证明:这条直线的方程可以写成
上一点,证明:这条直线的方程可以写成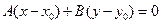 .
.
直线 和
和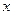 轴,
轴,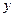 轴分别交于点
轴分别交于点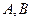 ,在线段
,在线段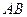 为边在第一象限内作等边△
为边在第一象限内作等边△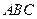 ,如果在第一象限内有一点
,如果在第一象限内有一点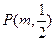 使得△
使得△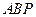 和△
和△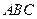 的面积相等,求
的面积相等,求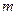 的值。
的值。
某学校共有教师 人,其中不到
人,其中不到 岁的有
岁的有 人,
人, 岁及以上的有
岁及以上的有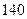 人。为了了解普通话在该校中的推广普及情况,用分层抽样的方法,从全体教师中抽取一个容量为
人。为了了解普通话在该校中的推广普及情况,用分层抽样的方法,从全体教师中抽取一个容量为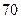 人的样本进行普通话水平测试,其中在不到
人的样本进行普通话水平测试,其中在不到 岁的教师中应抽取的人数为多少人?
岁的教师中应抽取的人数为多少人?
从两个班中各随机的抽取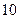 名学生,他们的数学成绩如下:
名学生,他们的数学成绩如下:
| 甲班 |
76 |
74 |
82 |
96 |
66 |
76 |
78 |
72 |
52 |
68 |
| 乙班 |
86 |
84 |
62 |
76 |
78 |
92 |
82 |
74 |
88 |
85 |
画出茎叶图并分析两个班学生的数学学习情况。
为了了解初三学生女生身高情况,某中学对初三女生身高进行了一次测量,所得数据整理后列出了频率分布表如下:
| 组 别 |
频数 |
频率 |
| 145.5~149.5 |
1 |
0.02 |
| 149.5~153.5 |
4 |
0.08 |
| 153.5~157.5 |
20 |
0.40 |
| 157.5~161.5 |
15 |
0.30 |
| 161.5~165.5 |
8 |
0.16 |
| 165.5~169.5 |
M |
n |
| 合 计 |
M |
N |
(1)求出表中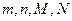 所表示的数分别是多少?
所表示的数分别是多少?
(2)画出频率分布直方图.
(3)全体女生中身高在哪组范围内的人数最多?