(本小题满分15分)已知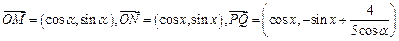
(1)当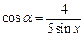 时,求函数
时,求函数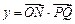 的最小正周期;
的最小正周期;
(2)当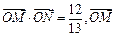 ∥
∥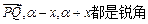 时,求
时,求 的值.
的值.
(本小题满分14分)某工厂三个车间共有工人1000名,各车间男、女工人数如下表:
| 第一车间 |
第二车间 |
第三车间 |
|
| 女工 |
173 |
100 |
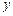 |
| 男工 |
177 |
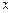 |
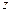 |
已知在全厂工人中随机抽取1名,抽到第二车间男工的概率是0.15.
(1)求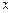 的值;
的值;
(2)现用分层抽样的方法在全厂抽取50名工人,问应在第三车间抽取多少名?
(3)已知 ,求第三车间中女工比男工少的概率.
,求第三车间中女工比男工少的概率.
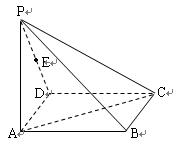
(本小题满分14分)如图ABCD是正方形,O是正方形的中心,PO 底面ABCD,E是PC的
底面ABCD,E是PC的
中点.求证:
(1)PA//平面BDE;
(2)平面PAC 平面BDE.
平面BDE.
(本小题为必做题,满分10分)已知数列 满足:
满足: .
.
(1) 求证: 使
使
(2) 求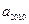 的末位数字.
的末位数字.
(本小题为必做题,满分10分)如图,在四棱锥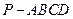 中,底面
中,底面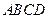 为矩形,侧棱
为矩形,侧棱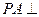 底面
底面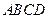 ,
,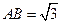 ,
,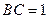 ,
,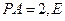 为
为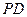 的中点.
的中点.
(1) 求直线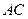 与
与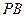 所成角的余弦值;
所成角的余弦值;
(2) 在侧面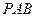 内找一点
内找一点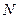 ,使
,使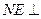 面
面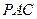 ,并求出点
,并求出点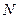 到
到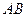 和
和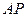 的距离.
的距离.