本题满分12分)
在直角坐标平面内,已知点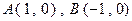 ,动点
,动点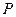 满足
满足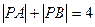 .
.
(1)求动点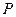 的轨迹
的轨迹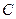 的方程;
的方程;
(2)过点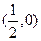 作直线
作直线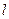 与轨迹
与轨迹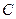 交于
交于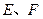 两点,线段
两点,线段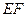 的中点为
的中点为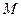 ,轨迹
,轨迹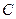 的右端点为点N,求直线MN的斜率
的右端点为点N,求直线MN的斜率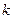 的取值范围.
的取值范围.
.椭圆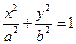
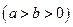 的两个焦点分别为
的两个焦点分别为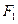 、
、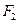 ,点
,点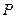 在椭圆
在椭圆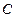 上,且
上,且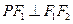 ,
,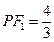 ,
,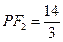 .
.
(1)求椭圆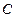 的方程;(2)若直线
的方程;(2)若直线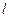 过圆
过圆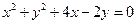 的圆心
的圆心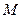 交椭圆于
交椭圆于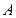 、
、 两点,且
两点,且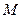 是
是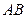 的中点,求直线
的中点,求直线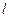 的方程.
的方程.
如图,正方形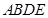 与等边
与等边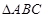 所在平面互相垂直,
所在平面互相垂直,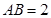 ,
,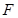 为
为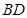 中点,
中点,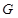 为
为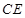 中点
中点
(1)求证: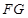 ∥平面
∥平面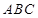 ;
;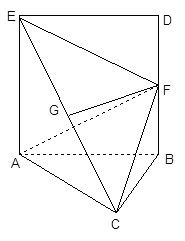
(2)求三棱锥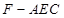 的体积.
的体积.
设命题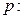 函数
函数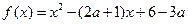 在
在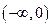 上是减函数;命题
上是减函数;命题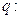 关于
关于 的方程
的方程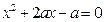 有实数根. 若命题
有实数根. 若命题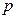 是真命题,命题
是真命题,命题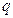 是假命题,求实数
是假命题,求实数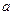 的取值范围.
的取值范围.
(本小题满分14分)
已知:椭圆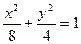 的左右焦点为
的左右焦点为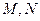 ;直线
;直线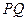 经过
经过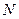 交椭圆于
交椭圆于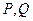 两点.
两点.
(1)求证: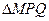 的周长为定值.
的周长为定值.
(2)求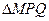 的面积的最大值?
的面积的最大值? 
(本小题满分14分)先后抛掷一枚骰子两次,将得到的点数分别记为 ,
, 。
。
(1)求 的概率;
的概率;
(2)求点 在函数
在函数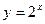 图像上的概率;
图像上的概率;
(3)将 的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率。
的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率。