已知定点A(-1,0),F(2,0),定直线l:x= ,不在x轴上的动点P与点F的距离是它到直线l的距离的2倍.设点P的轨迹为E,过点F的直线交E于B、C两点,直线AB、AC分别交l于点M、N
,不在x轴上的动点P与点F的距离是它到直线l的距离的2倍.设点P的轨迹为E,过点F的直线交E于B、C两点,直线AB、AC分别交l于点M、N
(Ⅰ)求E的方程;
(Ⅱ)试判断以线段MN为直径的圆是否过点F,并说明理由
如图,P为△ABC所在平面外一点,AP=AC,BP=BC,D为PC中点,直线PC与平面ABD垂直吗?为什么?
如图,D,E分别为三棱锥P—ABC 的棱AP、AB上的点,且AD:DP=AE:EB=1:3.求证:DE//平面PBC
的棱AP、AB上的点,且AD:DP=AE:EB=1:3.求证:DE//平面PBC
(本小题满分14分)有人玩掷正四面体骰子走跳棋的游戏,已知正四面体骰子四个面上分别印有 ,棋盘上标有第0站、第1站、第2站、…、第100站.一枚棋子开始在第0站,棋手每掷一次骰子,若掷出后骰子为
,棋盘上标有第0站、第1站、第2站、…、第100站.一枚棋子开始在第0站,棋手每掷一次骰子,若掷出后骰子为 面,棋子向前跳2站,若掷出后骰子为
面,棋子向前跳2站,若掷出后骰子为 中的一面,则棋子向前跳1站,直到棋子跳到第99站(胜利大本营)或第100站(失败大本营)时,该游戏结束.设棋子跳到第n站的概率为
中的一面,则棋子向前跳1站,直到棋子跳到第99站(胜利大本营)或第100站(失败大本营)时,该游戏结束.设棋子跳到第n站的概率为 (
( ).
).
(Ⅰ)求 ;
;
(Ⅱ)求证: ;
;
(Ⅲ)求玩该游戏获胜的概率.
(此题8、9、10班做)(本小题满分13分)
设数列 的前
的前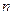 项和为
项和为 ,对一切
,对一切 ,点
,点 都在函数
都在函数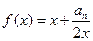 的图象上.
的图象上.
(Ⅰ)求 及数列
及数列 的通项公式
的通项公式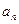 ;
;
(Ⅱ) 将数列 依次按1项、2项、3项、4项循环地分为(
依次按1项、2项、3项、4项循环地分为( ),(
),(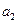 ,
, ),(
),(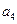 ,
,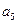 ,
, ),(
),( ,
,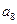 ,
,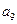 ,
,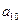 );(
);(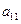 ),(
),(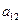 ,
,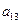 ),(
),( ,
,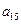 ,
, ),(
),( ,
, ,
, ,
,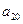 );(
);( ),…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为
),…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为 ,求
,求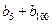 的值;
的值;
(Ⅲ)令 (
(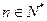 ),求证:
),求证: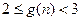 .
.
(此题平行班做)(本小题满分12分)
某班主任对全班50名学生的学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:

(Ⅰ)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是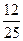 ,请完成上面的
,请完成上面的 列联表;
列联表;
 |
 |
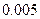 |
 |
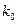 |
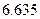 |
 |
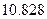 |
(Ⅱ)在(1)的条件下,试运用独立性检验的思想方法分析:在犯错误概率不超过0.1%的情况下判断学生的学习积极性与对待班级工作的态度是否有关?并说明理由.